| Ana Sayfa  | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

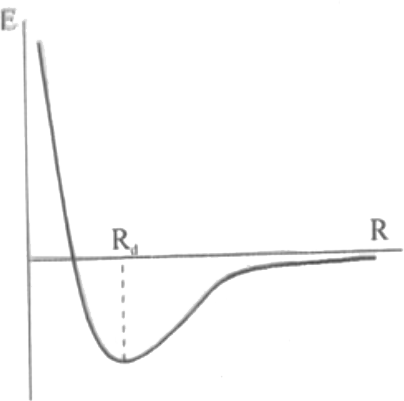
Moleküler Yapı Moleküler yapının kuantum kimyasal olarak çözümlenmesine en basit molekül olan hidrojen molekül iyonundan ( \rm H^+ ) başlayacağız. Böylece daha kompleks sistemlere doğru ilerlerken kullanılan yaklaşımları daha iyi anlayabileceğiz. \rm H_2 ^+ iki proton ve bir elektrondan oluşmuş bir moleküldür. Bu yapının kuantum kimyasal çözümü, bize bağ uzunlukları ve kimyasal yapıların davranışları konusunda önemli ip uçları verir. Born-Oppenheimer Yaklaşımı Born-Oppenheimer Yaklaşımına göre; çekirdekler elektronlara göre çok daha ağır olduklarından çok daha yavaş hareket ederler. Böylece elektronlar yerleri sabit çekirdekler etrafinda hareket ederler. Bu nedenle; çekirdeklerin birbirlerinden R kadar uzakta durduğu düşünülerek tek bir elektron için Schrödinger Eşitliğini çözebiliriz. Bu çözüm eşit durmdaki üç parçacık için Schrödinger Eşitliğini çözmekten çok daha kolaydır. Bu yaklaşım, normal haldeki moleküller için oldukça uygundur. Çünkü \rm H _2 ^+'daki çekirdekler 1 pm kadar hareket ederken, elektronlar 1000 pm hareket ederler. Bu nedenle çekirdeklerin pratik olarak durduğunu düşünmek pek yanlış olmayacaktır. \rm H _2 ^+ 'dan daha ağır çekirdekler için yaklaşım her zaman olmasa da daha iyidir. Born-Oppenheimer yaklaşımındaki tüm problem, birbirlerinden R kadar uzakta bulunan iki duran proton alanında bir elektron için Schrödinger Eşitliğinin çözümlenmesidir (Şekil 1). Bu alanda elektronun potansiyel enerjisi \rm V= -{ e^2 \over 4 \pi \epsilon _o} \Big( {1 \over r_A } + {1 \over r_B } \Big) \qquad \qquad (Eşitlik \; 1 ) Şekil 1 : \rm H _2 ^+'daki etkileşimler dir. Burada; \rm r_A \; ve \; r_B, A ve B çekirdeklerinden elektronun uzaklığıdır. Bu eşitlik tek-parçacık için Schrödinger eşitliğinin çözümlenmesinde kullanılabilir ve tam çözümler elde edilebilir. \rm - { \hbar ^2 \over 2m_e } \nabla \Psi + V \Psi = E \Psi \qquad \qquad (Eşitlik \; 2 ) Seçilmiş R mesafesinde molekülün toplam enerjisi özdeğer E'nin toplamıdır ve çekirdek çekirdek iteklemesi; \rm V_{çekirdek-çekirdek} = { e^2 \over 4 \pi \epsilon _o} { 1 \over R} \qquad \qquad (Eşitlik \; 3 ) Şekil 2 : Bir molekülün potansiyel enerji eğrisi. Minimum enerjiye karşı gelen denge bağ uzunluğu kadardır. Born-Oppenheimer yaklaşımı farklı R mesafeleri için çözüme izin verir ve elektron dağılımı bulunabilir. Bu yolla moleküllerin potansiyel enerji eğrisi elde edilebilir. Bu eğri üzerindeki en düşük değeri alan E için molekülün denge bağ uzunluğu hesaplanabilir. Molekül Orbital Yaklaşımı Schrödinger Eşitliğinin çözülmesiyle elde edilen bir elektronlu dalga fonksiyonları moleküler orbitaller olarak adlandırılır. Bir moleküler orbital \rm \Psi ise; moleküldeki elektron dağılımı \rm \Psi ^2 ile orantılıdır. Bir moleküler orbital atomik orbitale benzer. Fakat atomik orbitallerden farkı molekül boyunca sürmesidir. Tam analitik moleküler orbitaller Born- Oppenheimer yaklaşımı kullanılarak hidrojen molekül iyonu için elde edilebilir. Fakat bu orbitaller çok karmaşık orbitallerdir ve orbitallerin oluşumu ve enerjiye katkıları hakkında çok fazla bilgi vermez. Bu nedenle daha basit süreçler kullanacağız fakat bu süreçler daha yaklaşık olmakla birlikte daha fazla bilgi verecektir. Atomik Orbitallerin Lineer Kombinasyonu (Linear Combinations of Atomic Orbitals) (LCAO) Bu yaklaşımda, öncelikle elektron A çekirdeği etrafındayken Eşitlik (1)'deki \rm 1/r_A terimi \rm 1/r_B teriminden çok daha büyüktür. Bu nedenle Eşitlik (1)'deki \rm 1/r_B terimi ihmal edilebilir ve potansiyel enerji \rm V= -{ e^2 \over 4 \pi \epsilon _o} {1 \over r_A } \qquad \qquad (Eşitlik \; 4 ) olarak yazılabilir. Bu durumda; moleküldeki elektron için Schrödinger Eşitliği izole durumdaki H atomu ile aynıdır ve en düşük enerjili çözüm A üzerindeki 1s orbitalidir ve \rm \Psi _{1s} (A) şeklinde yazılabilir. Benzer şekilde B içinde moleküler orbital olarak \rm \Psi _{1s} (B) yazılabilir. Bu nedenle iki atomik orbitalin toplamı tüm dalga fonksiyonunu verecektir. \rm \Psi = N \big( \Psi _{1s} (A) + \Psi _{1s} (B) \big) \qquad \qquad (Eşitlik \; 5 ) Buradaki N, normalizasyon faktörüdür. Eşitlik 5 tipindeki bir toplam, teknik terim olarak atomik orbitallerin lineer kombinasyonu olarak adlandırılır. Atomik orbitallerin lineer kombinasyonlarından oluşan yaklaşık moleküler orbital ise LCAO-MO olarak adlandırılır. Soru 1 : Eşitlik (5) deki dalga fonksiyonunun Normalizasyon faktörünün değerini hesaplayınız. Çözüm: \rm \int \Psi ^2 d \tau = 1 olmalıdır. Değerleri yerine koyduğumuzda \rm N^2 \Big[ \int \big( \Psi _{1s} (A) \big)^2 d \tau + \int \big( \Psi _{1s} (B) \big)^2 d \tau + 2 \int \Psi _{1s} (A) \Psi _{1s} (B) d \tau \Big] = N^2(1+1+2S) olarak yazılabilir. Çünkü atomik orbitaller normalizedir. Bu nedenle normalizasyon faktörü, N; \rm N= { 1 \over 2^{1/2}(1+S)^{1/2} } olacaktır. Buradaki S overlap integrali olarak adlandırılır ve hidrojen molekül iyoundaki değeri 0.59 civarındadır. Böylece N = 0.56 olarak belirlenebilir. 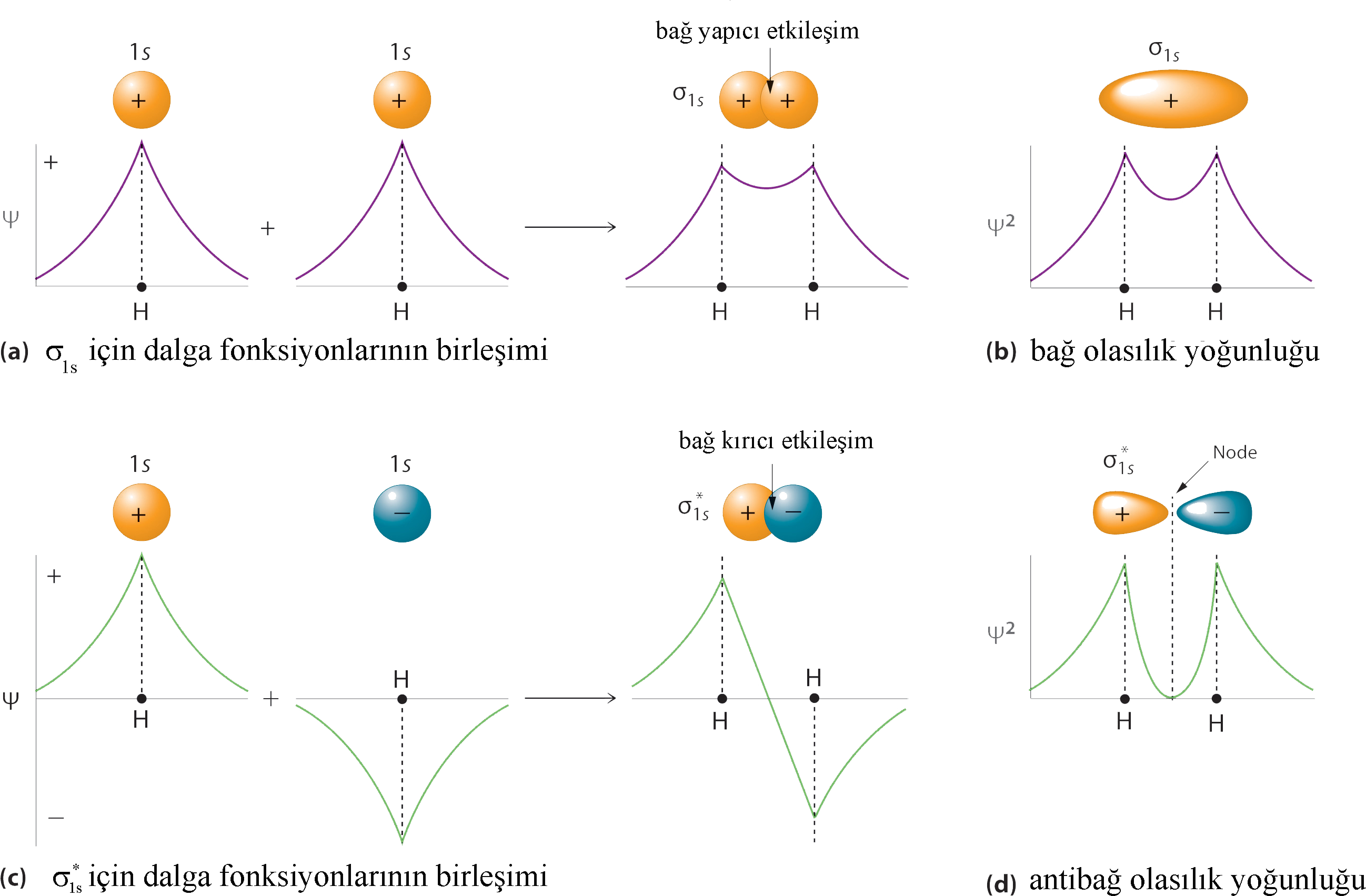Born yaklaşımına göre; \rm H_2 ^+ 'da elektronunn olasılık yoğunluğu dalga fonksiyonunun karesi ile orantılıdır. Eşitlik (5) deki LCAO-MO \rm 1s \sigma 'ın olasılık yoğunluğu; \rm \Psi ^2 = N^2 \big( \Psi _{1s} (A) + \Psi _{1s} (B) \big)^2 \qquad \qquad (Eşitlik \; 6 ) \rm \Psi ^2 = N^2 \Big[ \big( \Psi _{1s} (A) \big)^2 + \big( \Psi _{1s} (B) \big)^2 2 \int \Psi _{1s} (A) \Psi _{1s} (B) d \Big] \qquad \qquad (Eşitlik \; 7 ) yukarıdaki soruda görüldüğü gibi \rm H_2^+ ' da \rm N^2=0.31 olduğundan ve \rm \Psi _{1s} (A)= \Big( { 1 \over \pi a_o^3} \Big)^{1/2} e ^{-r_A /r_o} olduğundan ve benzer eşitlik B çekirdeği içinde yazılabileceğinden herhangi bir noktadaki dalga fonksiyonunun değeri ve olasılık yoğunluğu bulunabilir (Şekil 3). Şekil 3 : Hidrojen molekül iyonunda dalga fonksiyonu ve olasılık yoğunlukları Varyasyon (Variation) Prensibi Moleküler orbitallerin kurulmasında kullanılan lineer kombinasyonlardaki katsayıların bulunmasında sistematik olarak kullanılan yol varyasyon prensibiyle gerçekleştirilir. Varyasyon prensibine göre; eğer keyfi bir dalga fonksiyonu enerji hesaplamada kullanılıyorsa, hesaplanan değer gerçek enerjiden daha az değildir. Keyfi dalga dalga fonksiyonları deneme (trial) dalga fonksiyonları olarak adlandırılır. Bir başka deyişle bu prensip; eğer en düşük enerji değerine ulaşılıncaya kadar deneme dalga fonksiyonlarındaki katsayıları değiştirirsek, en düşük enerji değerini veren katsayılar en iyi katsayılardır. Bu yönteme göre deneme dalga fonksiyonu \rm \Psi = c_A \Psi(A)+ c_B \Psi(B) \qquad \qquad (Eşitlik \; 8 ) şeklinde gösterilebilir. Bu fonksiyon gerçektir fakat katsayılar keyfi olarak alındığından normalize değildir. Bu nedenle \rm \int \Psi ^2 d \tau =1 olarak alınamaz. Orbitalin enerjisi enerji operatöründen beklenen değerdir. \rm E = { \int \Psi H \Psi d \tau \over \Psi^2 d \tau} \qquad \qquad (Eşitlik \; 9 ) Bu noktadan sonra E'nin minimum yapan değerlere ulaşmak için deneme fonksiyonlarındaki katsayıların değerleri araştırılmalıdır. Bu hesaplamada standart bir yoldur ve katsayıları çözmek için; \rm { \partial E \over \partial c_A}=0 \; ve \; { \partial E \over \partial c_B}=0 \qquad \qquad (Eşitlik \; 10 ) değerleri belirlenmelidir. Secular Eşitlikler Eşitlik 8 daki dalga fonksiyonu kullanılarak Eşitlik 9 daki payda için; \rm \int \Psi ^2 d \tau = \int { \big( c_A \Psi (A) + c_B \Psi (B) \big)^2 d \tau } \qquad \qquad (Eşitlik \; 11 ) \rm \int \Psi ^2 d \tau = c_A^2 \int \big( \Psi (A) \big)^2 d \tau + c_B^2 \int \big( \Psi (B) \big)^2 d \tau + 2 c_A c_B \int \Psi (A) \Psi (B) d \tau \qquad \qquad (Eşitlik \; 12 ) \rm \int \Psi ^2 d \tau = c_A ^2 + c_B^2 + 2 c_A c_B S \qquad \qquad (Eşitlik \; 13 ) yazılabilir. Çünkü tek başlarına atomik orbitaller normalizedirler ve üçüncü integral overlap integralidir. Pay ise; \rm \int \Psi H \Psi d \tau = \int \big( c_A \Psi (A) + c_B \Psi (B) \big) H \big( c_A \Psi (A) + c_B \Psi (B) \big) d \tau \qquad \qquad (Eşitlik \; 14 ) \rm \int \Psi H \Psi d \tau = c_A^2 \int \Psi (A) H \Psi (A) d \tau + c_B^2 \int \Psi (B) H \Psi (B) d \tau + 2c_A c_B \int \Psi (A) H \Psi (B) \qquad \qquad (Eşitlik \; 15 ) Bu eşitlikteki integraller karmaşık gözükmesine karşın, bu integraller yerine sabitler kullanılabilir. \rm \alpha _A = \int \Psi (A) H \Psi (A) d \tau \qquad \qquad (Eşitlik \; 16 ) \rm \alpha _B = \int \Psi (B) H \Psi (B) d \tau \qquad \qquad (Eşitlik \; 17 ) \rm \beta = \int \Psi (A) H \Psi (B) \qquad \qquad (Eşitlik \; 18 ) Böylece \rm \int \Psi H \Psi d \tau = c_A^2 \alpha _A + c_B^2 \alpha _B + 2 c_A c_B \beta \qquad \qquad (Eşitlik \; 19 ) \rm \alpha ; Coulomb integrali olarak adlandırılır. Negatif bir değere sahiptir ve \rm \alpha _A için \rm \Psi (A) ya da \rm \alpha _B için \rm \Psi (B) orbitali dolduğunda elektronun enerjisi anlamına gelir. Homonükleer diatomik moleküller için \rm \alpha _A = \alpha _B dir. \rm \beta ; klasik nedenlerle rezonans integrali olarak adlandırılır. Orbitaller üst üste binmedikleri zaman ortadan kaybolur ve denge bağ uzunluklarında negatif değere sahiptir. E için eşitlik böylece; \rm E = { c_A^2 \alpha _A + c_B^2 \alpha _B + 2 c_A c_B \beta \over c_A ^2 + c_B ^2 + 2 c_A c_B S} \qquad \qquad (Eşitlik \; 20 ) dir. Minimum değerin bulunması için iki kaysayıya göre difransiyel alınırsa iki secular eşitlik meydana gelir. Bunlar; \rm \big( \alpha _A -E \big) c_A + \big( \beta -ES \big)c_B = 0 \rm \big( \beta -ES \big)c_A + \big( \alpha _B -E \big) c_B = 0 dır. Bu noktadan sonra katysayıların ortaya çıkartılabilmesi için secular determinant \rm \left| \, \matrix{ ( \alpha _A -E ) & ( \beta -ES ) \cr ( \beta -ES ) & ( \alpha _B - E) } \right| = 0 şeklinde kurulabilir. Determinanttaki eğer aynı iki çekirdekten söz ediliyorsa \rm \alpha _A = \alpha _B = \alpha yazılabileceğinden determinantın kökleri \rm \left| \, \matrix{ ( \alpha -E ) & ( \beta -ES ) \cr ( \beta -ES ) & ( \alpha - E) } \right| = ( \alpha -E)^2 - ( \beta -ES)^2 =0 \rm E _+ = { \alpha + \beta \over 1 + S } \qquad E _- = { \alpha - \beta \over 1 - S } olarak belirlenebilir. En iyi katsayılar için dalga fonksiyonu normalize olacağından Eşitlik (19) 'deki tüm bölge için olasılık yoğunluğu \rm \int \Psi ^2 d \tau = c_A^2 + c_B^2 + 2c_Ac_BS = 1 olacaktır. İki atom aynı olduğundan \rm E_+ = { \alpha + \beta \over 1 + S } \qquad c_A = \Big( { 1 \over 2 (1+S)} \Big)^2 \qquad c_A =c_B \rm E_- = { \alpha - \beta \over 1 - S } \qquad c_A = \Big( { 1 \over 2 (1-S)} \Big)^2 \qquad c_A =-c_B çözümleri elde edilebilir. Bu olay için en iyi bağ oluşumunu sağlayan fonksiyon \rm \Psi _+ = \Big( { 1 \over 2 (1+S) } \Big)^{1/2} \big( \Psi (A) + \Psi (B) \big) \rm \Psi _- = \Big( { 1 \over 2 (1-S) } \Big)^{1/2} \big( \Psi (A) - \Psi (B) \big) dır. 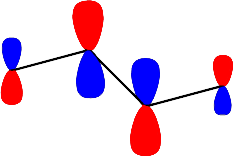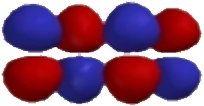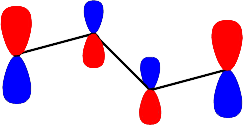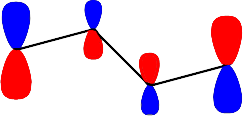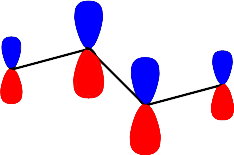Overlap integrali S rezonans integrali \rm \beta ile \rm \beta = \kappa S şeklinde ilişkilidir. Hückel Moleküller Orbital Yaklaşımı Konjuge moleküllerin \rm \pi moleküler enerji seviyesi diagramları Erich Hückel tarafından önerilen yaklaşımlar kullanılarak kurulmuştur. Bu yaklaşımda, \rm \pi orbitalleri molekülün şeklini belirleyen iskelet oluştuktan sonra ve \rm \alpha \rm \alpha olarak alınabilir. Örneğin bütadiendeki 2p orbitallerinin lineer kombinasyonu \rm \matrix{ (1) & & (2) & & (3) & & (4) \cr H_2C & = & CH & - & CH & = &CH_2 } \rm \Psi = c_1 \Psi (1) + c_2 \Psi (2) + c_3 \Psi (3) + c_4 \Psi (4) olarak yazılabilir. Bütadien için seküler determinant \rm \left| \matrix{ \alpha -E & \beta _{12} -ES_{12} & \beta _{13} -ES_{13} & \beta _{14} -ES_{14} \cr \beta _{21} -ES_{21} & \alpha -E & \beta _{23} -ES_{23} & \beta _{24} -ES_{24} \cr \beta _{31} -ES_{31} & \beta _{32} -ES_{32} & \alpha -E & \beta _{34} -ES_{34} \cr \beta _{41} -ES_{41} & \beta _{42} -ES_{42} & \beta _{43} -ES_{43} & \alpha -E } \right| =0 olarak yazılabilir. Bu determinantdaki rezonans integralleri ve overlap integralleri bilgisayarlar kullanılarak çözülebilir. Fakat moleküler enerji seviyeleri, daha kabaca da olsa aşağıdaki Hückel yaklaşımları kullanılarak daha kolay hesaplanabilir. Tüm overlap integrallerinin değeri sıfıra eşittir. Komşu olmayan atomlar arasındaki tüm rezonans integralleri sıfıra eşittir. Tüm rezonans integralleri \rm \beta 'ya eşittir. Bu yaklaşımlar doğrultusunda yukarıdaki determinant \rm \left| \matrix { \alpha -E & \beta & 0 & 0 \cr \beta & \alpha -E & \beta & 0 \cr 0 & \beta & \alpha -E & \beta \cr 0 & 0 & \beta & \alpha -E } \right| =0 \rm \left| \matrix { { \alpha -E \over \beta} & 1 & 0 & 0 \cr 1 & { \alpha -E \over \beta} & 1 & 0 \cr 0 & 1 & { \alpha -E \over \beta} & 1 \cr 0 & 0 & 1 & { \alpha -E \over \beta} } \right| =0 \rm \left| \matrix { X & 1 & 0 & 0 \cr 1 & X & 1 & 0 \cr 0 & 1 & X & 1 \cr 0 & 0 & 1 & X } \right| =0 şeklinde tekrar düzenlenebilir. Burada; \rm X = {\alpha - E \over \beta } dır. X değerlerinin bulunması ile enerji seviyeleri bulunabilir. \rm X \left| \matrix { X & 1 & 0 \cr 1 & X & 1 \cr 0 & 1 & X \cr } \right| - \left| \matrix { 1 & 1 & 0 \cr 0 & X & 1 \cr 0 & 1 & X \cr } \right| =0 \rm X^2 \left| \matrix { X & 1 \cr 1 & X } \right| - X \left| \matrix { 1 & 1 \cr 0 & X } \right| - \left| \matrix { X & 1 \cr 1 & X } \right| + \left| \matrix { 0 & 1 \cr 0 & X } \right| =0 \rm X^2(X^2-1)-X^2-(X^2-1)=0 \rm X^4-3X^2+1=0 \rm Y = X^2 dersek; \rm Y^2-3Y+1=0 yazabiliriz ki buradan \rm Y_1=2.618033989 \; Y_2=0.381966011 Böylece; \rm X_{1,2}= \pm 1.61804 \qquad X_{3,4} = \pm 0.61804 olarak elde edilebilir. \rm X = {\alpha - E \over \beta } olduğundan \rm 4 \pi elektronu aşağıdaki enerji seviyelerinde bulunur. Şekil 4 : Bütadien molekülündeki \rm \pi elektronlarının \rm \pi orbitallerini doldurması. Bütadien molekülündeki Atomik Orbital Katsayıları Bütadien molekülündeki herhangi bir Xi enerji seviyesine sahip molekül orbitaldeki katsayılar \rm X_ic_1+c_2=0 \rm c_1+X_ic_2+c_3=0 \rm c_2+X_ic_3+c_4=0 \rm c_3+X_ic_4=0 \rm c_1^2+c_2^2+c_3^2+c_4^2=1 denklemlerinin çözülmesi ile elde edilebilirler. Fakat özellikle moleküllerin büyümesi ile bu denklemlerin çözülmesi karmaşıklaşır ve bilgisayar gerektirmeye başlar. Bu nedenle daha basit bir yöntemle dalga fonksiyonudaki katsayılar belirlenebilir. Bu yöntem eşçarpan yöntemi olarak adlandırılır. Eşçarpan Metodu: Moleküler orbitallerin dalga fonksiyonlarının katsayılarının bulunmasında kullanılan bir yöntemdir. Eşçarpan motodu ile normalize dalga fonksiyonları elde edilir fakat bu yöntem dejenere enerji seviyeleri için kullanılmaz. Eşçarpan medotuna göre; moleküler orbital dalga fonksiyonunda bulunan i. atomun katsayısı \rm c_i, seküler determinantın birinci ve herhangi bir sırasının i. elemanının eşçarpanı \rm A_i ile orantılıdır. Birinci satırın \rm a_{11} elemanının eşçarpanı \rm c_i \sim A_i = (-1)^{1+i}(Minör)_{11} dır. Bu eşitlikte \rm (Minör)_{11} birinci satırın i. elemanı \rm a_{11} 'nin bulunduğu satır ve sütünlar kaldırıldıktan sonra geriye kalan alt determinantı göstermektedir. \rm c_i katsayısı; \rm c_i = { A_i \over (\sum{ A_i ^2})^{1/2} } eşitliği ile hesaplanır. Moleküldeki her atomun \rm c_i katsayısı ayrı ayrı her enerji seviyesi için hesaplandığından sonuçların bir tabloda toplanması kolaylık sağlar. Eşçarpan metodunun uygulanışı, bütadien molekülü için aşağıda gösterilmiştir. Seküler determinantın birinci satırındaki elemanların eşçarpanları \rm A_1 = \left| \matrix { X & 1 & 0 \cr 1 & X & 1 \cr 0 & 1 & X } \right| = X \left| \matrix { X & 1 \cr 1 & X } \right| - \left| \matrix { 1 & 1 \cr 0 & X } \right| = X^3-2X \rm A_2 =- \left| \matrix { 1 & 1 & 0 \cr 0 & X & 1 \cr 0 & 1 & X } \right| = - \left| \matrix { X & 1 \cr 1 & X } \right| + \left| \matrix { 0 & 1 \cr 0 & X } \right| = X^2+1 \rm A_3 =- \left| \matrix { 1 & X & 0 \cr 0 & 1 & 1 \cr 0 & 0 & X } \right| = \left| \matrix { 1 & 1 \cr 0 & X } \right| -X \left| \matrix { 0 & 1 \cr 0 & X } \right| = X \rm A_4 =- \left| \matrix { 1 & X & 1 \cr 0 & 1 & X \cr 0 & 0 & 1 } \right| = - \left| \matrix { 1 & X \cr 0 & 1 } \right| +X \left| \matrix { 0 & X \cr 0 & 1 } \right| - \left| \matrix { 0 & 1 \cr 0 & 0 } \right| =0 dir. Herbir enerji seviyesi için dalga fonksiyonları \rm \Psi \; (E_1) \; için; \; X = -1.618; E_1 = \alpha + 1.618 \beta i \rm A_i \rm A_i^2 \rm c_i 1 -0.999 0.996 -0.371 2 -1.617 2.614 -0.601 3 -1.618 2.617 -0.601 4 -1.000 1.000 -0.317 \rm \sum A_i^2 =7.230 \rm \big( A_i^2 \big)^{1/2} = 2.688 katsayıların hepsi de aynı işaretli olduğundan bağ yapıcı bir orbital. olduğunu gösterir. Moleküler dalga fonksiyonu ise; \rm \Psi (E_1) = 0.371 \Psi _1 + 0.601 \Psi _2 + 0.601 \Psi _3 + 0.371 \Psi _4 olarak yazılabilir. İkinci enerjii seviyesini gösteren dalga fonksiyonu; \rm \Psi \; (E_2) \; için; \; X = -0.618; E_2 = \alpha + 0.618 \beta i \rm A_i \rm A_i^2 \rm c_i 1 -0.999 0.998 0.601 2 -1.618 0.381 0.371 3 -1.618 0.381 -0.371 4 -1.000 1.000 -0.601 \rm \sum A_i^2 =2.761 \rm \big( A_i^2 \big)^{1/2} = 1.661 \rm \Psi (E_2)= 0.601 \Psi _1 + 0.371 \Psi _2 -0.371 \Psi _3 -0.601 \Psi _4 Üçüncü enerjii seviyesini gösteren dalga fonksiyonu; \rm \Psi \; (E_3) \; için; \; X = 0.618; E_3 = \alpha - 0.618 \beta i \rm A_i \rm A_i^2 \rm c_i 1 -0.999 0.998 -0.601 2 0.618 0.381 0.371 3 0.618 0.381 -0.371 4 -1.000 1.000 -0.601 \rm \sum A_i^2 =2.761 \rm \big( A_i^2 \big)^{1/2} = 1.661 \rm \Psi (E_3)= -0.601 \Psi _1 + 0.371 \Psi _2 +0.371 \Psi _3 -0.601 \Psi _4 Dördüncü enerjii seviyesini gösteren dalga fonksiyonu; \rm \Psi \; (E_4) \; için; \; X = 1.618; E_4 = \alpha - 1.618 \beta i \rm A_i \rm A_i^2 \rm c_i 1 0.999 0.996 -0.371 2 -1.617 2.614 -0.601 3 1.618 2.617 -0.601 4 -1.000 1.000 -0.371 \rm \sum A_i^2 =7.227 \rm \big( A_i^2 \big)^{1/2} = 2.688 Moleküler dalga fonksiyonu ise; \rm \Psi (E_4)= 0.371 \Psi _1 - 0.601 \Psi _2 +0.601 \Psi _3 -0.371 \Psi _4 olarak yazılabilir. Bütadien Molekülündeki Yük Yoğunlukları Moleküler orbital dalga fonksiyonlarının kullanılması ile molekülün elektrik yükü ve bu yükün yoğun olduğu noktalar hesaplanabilir. A ve B atomlarından oluşmuş bir molekülün dalga fonksiyonunun; \rm \int \Psi ^2 d \tau = \int { \big( c_A \Psi (A) + c_B \Psi (B) \big)^2 d \tau } \rm \int \Psi ^2 d \tau = c_A^2 \int \big( \Psi (A) \big)^2 d \tau + c_B^2 \int \big( \Psi (B) \big)^2 d \tau + 2 c_A c_B \int \Psi (A) \Psi (B) d \tau \rm \int \Psi ^2 d \tau = c_A ^2 + c_B^2 + 2 c_A c_B S olduğunu daha önce görmüştük. Ayrıca Hückel molekül orbital yaklaşımına göre ifadedeki son terimin s:fi olduğundan bahsetmiştik. Buradaki \rm c_A^2 \; ve \; c_B^2 katsayıları sırası ile A ve B atomu üzerinde bulunan elektron yoğunluğudur. Moleküler herhangi bir atomunun toplam eletron yoğunluğu ise dolu olan moleküler orbitallerdeki her elektronun yoğunluk katkıları toplamıdır. Bu nedenle A atomu üzerindeki elektron yoğunluğu \rm q_A ; \rm q_A = \sum ^{ \Psi _{ dolu }} n c_A ^2 \qquad \qquad (Eşitlik \; 21 ) dir. \rm q_A, A atomunun elektron yoğunluğu olduğundan A atomunun yük yoğunluğu Z_A 'da; \rm Z_A = 1.000- q_A = 1.000 - \sum ^{ \Psi _{ dolu }} n c_A ^2 \qquad \qquad (Eşitlik \; 22 ) eşitliği ile gösterilebilir. Dalga fonksiyonlarını ve elektron doluluk durumlarını tekrar özet olarak yazalım. Dalga Fonksiyonu Enerjisi Atomik Orbitaller Moleküler Orbitaller Durumu Table : Bütadiendeki dalga fonksiyonları ve enerjileri \rm \Psi (E_4)= 0.371 \Psi _1 - 0.601 \Psi _2 +0.601 \Psi _3 -0.371 \Psi _4 \rm E_4 = \alpha - 1.618 \beta Boş orbital \rm \Psi (E_3)= -0.601 \Psi _1 + 0.371 \Psi _2 +0.371 \Psi _3 -0.601 \Psi _4 \rm E_3 = \alpha - 0.618 \beta Boş orbital LUMO orbitali \rm \Psi (E_2)= 0.601 \Psi _1 + 0.371 \Psi _2 -0.371 \Psi _3 -0.601 \Psi _4 \rm E_2 = \alpha + 0.618 \beta iki elektron ile dolu HOMO orbitali \rm \Psi (E_1) = 0.371 \Psi _1 + 0.601 \Psi _2 + 0.601 \Psi _3 + 0.371 \Psi _4 \rm E_1 = \alpha + 1.618 \beta iki elektron ile dolu En düşük enerjili orbital Bu nedenle bütadien molekülü için elektron yoğunluğu ve yük yoğunlukları ilk iki orbital 2 'şer elektron ile dolu olduğundan \rm q_1=2[(0.371)^2+(0.601)^2] = 0.998 \simeq 1.000 \qquad \qquad Z_1=1.000-1.000 = 0 \rm q_2=2[(0.601)^2+(0.371)^2] = 0.998 \simeq 1.000 \qquad \qquad Z_2=1.000-1.000 = 0 \rm q_3=2[(0.601)^2+(-0.371)^2] = 0.998 \simeq 1.000 \qquad \qquad Z_3=1.000-1.000 = 0 \rm q_4=2[(0.371)^2+(-0.601)^2] = 0.998 \simeq 1.000 \qquad \qquad Z = 1.000-1.000 = 0 olarak elde edilebilir. Bütadien Molekülündeki Bağ Mertebeleri Hückel moleküler orbital yaklaşımına göre \rm \sigma bağları lokalize bağlar olduklarından iki atom arasında tek bir bağ varsa bağ mertebesi l'dir. Fakat çifte bağlı molekülerde özellikle konjügasyon durumuda varsa \rm \pi elektronları moleküldeki atomların tamamını etkileyecek şekilde hareket ederler. Bu nedenle; \rm \pi elektronlarının yoğunlukları bazı atomlar arasında fazla bazı atomlar arasında ise daha az olur. İki atom arasındaki \rm \pi elektron yoğunluğuna hareketli bağ mertebesi denir. A ve B atomları arasındaki hareketli bağ mertebesi \rm P_{AB} = \sum ^{ \Psi _{ dolu }} n c_A c_B \qquad \qquad (Eşitlik \; 23 ) şeklinde ifade edilir. A ve B atomları arasındaki moleküler orbital bağ yapıcı ise \rm P_{AB} pozitif, non-bonding bir orbital ise sıfır, antibağ orbitali ise negatiftir. İki atom arasında \rm \sigma bağ mertebesi 1.000 olduğundan, toplam bağ mertebesi \rm N_{AB}; \rm N_{AB} = 1.000 + P_{AB} \qquad \qquad (Eşitlik \; 24 ) dir. Bu durumda bütadien molekülündeki hareketli: bağ mertebeleri ve toplam bağ mertebeleri \rm P_{12} = 2[(0.371)(0.601) + (0.601)(0.371)] = 0.892 \qquad \qquad N_{12} = 1.892 \rm P_{23} = 2[(0.601)(0.601)+(0.371)(-0.371)] = 0.447 \qquad \qquad N_{23} = 1.447 \rm P_{34} = 2[(0.601)(0.371) + (-0.371)(-0.601)] = 0.892 \qquad \qquad N_{34} = 1.892 dir.