| Ana Sayfa  | Özgeçmiş | Çalışmalar | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

Schrödinger Atom Modeli

Bohr, atom modelini kuantum teorisinden geliştirdiği gibi, dalga mekaniğine göre atom modeli de Brogli'nin parçacığın dalga özelliğine sahip olduğunu kabul etmesinden yararlanarak geliştirilmiştir. Bu model elektronları atom çekirdeği etrafında nasıl düzenlendiklerini ayrıntıları ile gösterir. Atomik spektrumlardaki tüm çizgileri de problemsiz olarak açıklar. Daha önce \rm E = h \upsilon Planck kuantum kuramında değinmiştik. Ayrıca \rm v = c / \lambda olduğundan; \rm E = h { c \over \lambda } (1) yazılabilir. \rm E = mc^2 / \lambda olduğundan \rm E = mc^2 = h { c \over \lambda } (2) Böylece bir parçacığa eşlik eden dalgaboyu; \rm \lambda = { h \over mc } = { h \over p } (3) Burada p fotonun momentumu olup p = mc dir. 1925 yılında de Broglie elektrona ait dalganın dalga boyunun \lambda = { h \over m v } olarak verilebileceğini gösterdi. 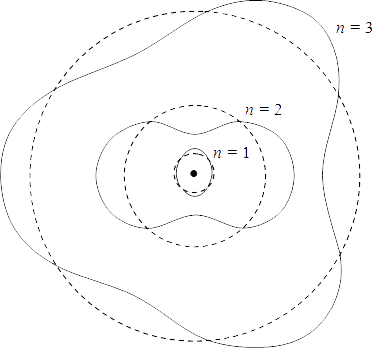Bu sonuç Bohr Atom Teorisine uygulanırsa; m v r = n { h \over 2 \pi } eşitliğini düzenlersek ; 2 \pi r = n { h \over m v } = n \lambda (4) yazabiliriz. Bu bir Bohr yörüngesindeki elektrona eşlik eden dalga boyunun yörüngenin çevresine eşit veya tam katları olması gerektiğini söyler. (A)                                (B) Şekil 1 : (A) de Broglie Eşitliğine göre bir atom etrafındaki elektrona eşlik eden dalgaların olası durumu. (B) de Broglie Eşitliğine göre bir atom etrafındaki elektrona eşlik eden dalgaların yasaklanmış durumu. De Broglie'nin modeli; Schrödinger'i atom içindeki elektronların davranışlarını bir hal fonksiyonu ile ifade edebileceği ve denklemin çözümü ile atom hakkıda pekçok bilgiye ulaşılabileceği fikrine götürdü. Schrödingere göre bir x doğrultusunda hareket eden tanecik için bu denklem { h^2 \over 8 \pi^2 m } { \partial^2 \Psi \over \partial^2 \chi } + V \Psi = E \Psi (5) şeklindedir. Buradaki \rm \Psi ; taneciğe eşlik eden dalga fonksiyonu, V ; potansiyel enerji operatörü, E : taneciğin sahip olduğu toplam enerjidir. Gerçek sistemler için denklem çözülmeye çalışılırsa bazı kuantum sayıları olarak adlandırılan tam sayılar olmaksızın denklemin çözümü anlamsızdır. Bu nedenle kuantlaşmış enerji ve kuantum sayıları Schrödinger Teorisinin doğal sonuçları olmuştur. Schrödinger denklemini gerçek sistemlere uygularken dalga fonksiyonunu radial ve açısal kısımlara parçalamak gerekir. Bu durum için dalga fonksiyonu \Psi (r, \theta, \phi ) = R(r) \cdot \Theta ( \theta) \cdot \Phi ( \phi ) (6) şeklinde ifade edilir. Buradaki R(r) dalga fonksiyonun radial kısmını, \Theta ( \theta) \cdot \Phi ( \phi ) , ise açısal kısmını gösterir. Daha fazla bilgi için kuantum kimyası notlarına bakabilirsiniz. de Broglie Dalgaları İle İlgili Etkileşimli Sorular Bir parçacığa eşlik eden dalgaboyu