| Ana Sayfa  | Özgeçmiş | Çalışmalar | Dersler | Ders Programı | Simülasyonlar  | Diğer | İletişim |

Elektronların Atomik Orbitalleri Doldurmaları

Schrödinger Denkleminin çözümü elektronların orbitalere nasıl dağılacağı konusunda bilgi verir. Elektronların atomda çekirdek etrafında nasıl dizildiğini ve bunu belirleyen kuralları anlamak için atomdaki enerji düzeylerini ve bunları belirlemek için kullanılan kuantum sayılarını bilmek gerekir. Schrödinger denkleminin çözümüne göre bu kuantum sayıları baş kuantum sayısı n, yan kuantum sayısı l ve magnetik kuantum sayısı ml dir. Bu kuantum sayısından başka son bir kuantum sayısı ise spin kuantum sayısı s dir. I. Baş (Birincil) Kuantum Sayısı (n) Bohr kuantum kuramında olduğu gibi n; 1, 2, 3, ... değerleri alabilir. Sayıların yanısıra tabakaları göstermek için harflerde kullanılır. n = 1 ise bu birinci enerji seviyesini, n = 2 ise ikinci enerji seviyesini gösterir. Tablo 1 de baş kuantum sayıları ve karşı gelen kabuk isimleri gösterilmiştir. Tablo 1 : Baş kuantum sayısı ve kabuklar Baş Kuantum Sayısı (n) 1 2 3 4 5 ... Tabakalar K L M N O ... II. Yan (İkincil) Kuantum Sayısı (l) Baş kuantum sayısı ile tanımlanmış enerji seviyelerinin daha alt enerji seviyeleri içerir. Bir enerji seviyesindeki alt enerji seviyelerinin sayısı n - 1 tanedir. Örneğin; n = 1 ise; alt enerji seviyelerinin l = 1 - 1 = 0 dir. Bunun anlamı bir enerji seviyesi bulunur demektir. n = 2 için ; l = 2 - 1 = 1 olup bir alt enerji seviyesi bulunması anlamına gelir. Bir başka deyişle 2 enerji seviyesi seviyesi bulundurur demektir. Bir tabakadaki tabakaların sayısı baş kuantum sayısına eşittir. Alt tabakaları göstermek içinde harf kullanılır. Tablo 2 : Yan (İkincil) kuantum sayısı ve alt kabukların adları. Yan Kuantum Sayısı (l) 0 1 2 3 ... Alt Tabakalar s p d f ... Şekil 1 : Orbital enerjileri. III. Manyetik Kuantum Sayısı ml Her alt tabaka ise bir veya daha fazla eş enerjili dejenere orbitalden oluşmuştur. Herbir alt tabakadaki her bir yörünge magnetik kuantum sayısı ml ile gösterilir. Magnetik kuantum sayısının aldığı değerler yan kuantum sayısının değerine göre \rm \pm l değerlerini alır. Bu nedenle herbir alt tabakadaki aldığı değer sayısı ikincil kuantum sayısına bağlı olarak 2l+1 eşitliği ile verilir. Örneğin; l = 0 ise ; ml = 0 değerini alır. l = 1 ise; ml = -1 , 0 , +1 l = 2 ise; ml = -2, -1, 0, +1, +2 değerlerini alır. Enerji seviyeleri, alt enerji seviyeleri ve yörüngeler enerji düzeyleri için; Tabakların enerjileri, kuantum sayısı n artmasıyla artar. Kuantum sayısı n arttıkça tabakalar arasındaki enerji farkı azalmaktadır. Çok elektronlu sistemlerde 3. enerji seviyesinden başlayarak alt tabakalarının enerji değerlerinin birbirine karıştığı gözlenir. Schrödinger denkleminin bir sonucu olarak elde edilen kuantum sayıları Tablo 3 de gösterilmiştir. Ayrıca Şekil 2 de de orbitallerin şekilleri görülmektedir. Tablo 3 : Schrödinger denklemin sonucu elde edilen kuantum sayılarının atomdaki dağılımı. Birincil (Baş) Kuantum Sayısı İkincil (Yan) Kuantum Sayısı Manyetik Kuantum Sayısı ml Alt Tabakadaki Yörünge Sayısı n Tabaka Adı l Alt Tabaka 1 K 0 1s 0 1 2 L 0 1 2s 2p 0 -1 0 +1 1 3 3 M 0 1 2 3s 3p 3d 0 -1 0 +1 -2 -1 0 +1 +2 1 3 5 4 N 0 1 2 3 4s 4p 4d 4f 0 -1 0 +1 -2 -1 0 +1 +2 -3 -2 -1 0 +1 +2 +3 1 3 5 7 Şekil 2 : s, p, d, f orbitalleri. Şekil 3 : Elektronlar ve spinleri. IV. 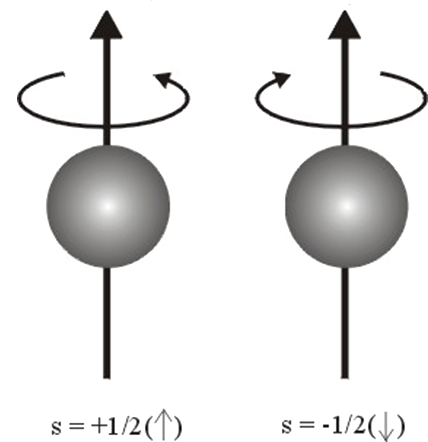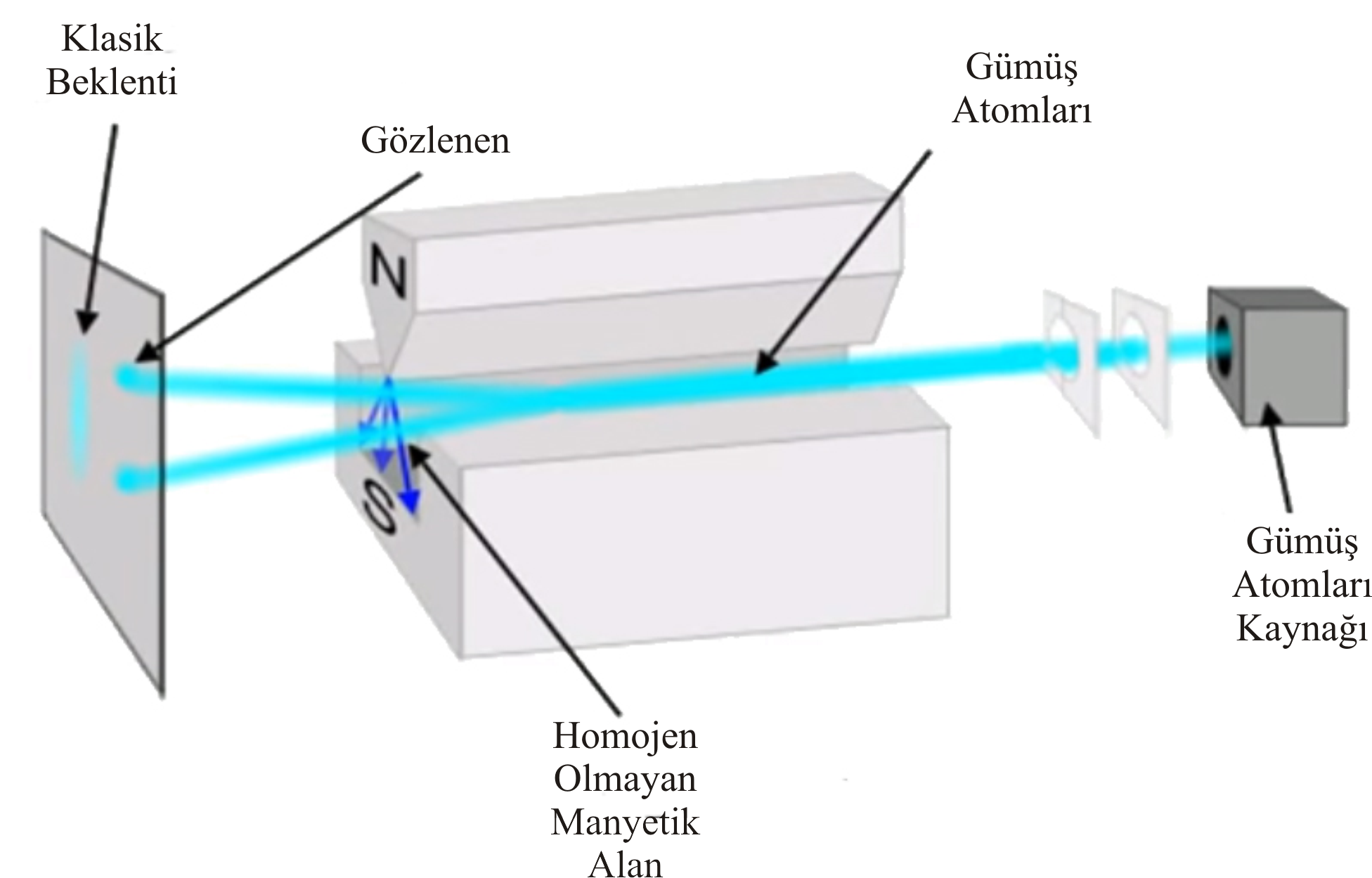Spin Kuantum Sayısı (s) Spin Kuantum Sayısı (ms), bir elektronun açısal momentumunu tanımlar. Bir elektron bir eksen etrafında dönerken ve hem açısal momentuma hem de yörünge açısal momentuma sahip olur. Açısal momentum bir vektör olduğundan, Spin Kuantum Sayısının (s) büyüklüğü \rm \pm {1 \over 2} dir (Şekil 3). Bu öneri için denel kanıt, O. Stern ve W. Gerlach tarafından verilmiştir. Deneyde, gümüş metal buharı ince bir demet halinde güçlü bir magnetik alandan geçirilmiştir. Gümüş atomunda en dış yörüngede bir tek elektron vardır ve magnetik alandan geçen gümüş atomlarının iki yöne ayrıldıkları görülmüştür (Şekil 4). Bunun nedeni; dönen yüklü taneciğin magnetik özellik göstermesinden kaynaklanır. Elektron küçük bir mıknatıs gibi davranır ve elektronun iki türlü dönme hareketi zıt yönlenmiş iki mıknatıs oluşturur. O halde spinleri zıt olan elektronları taşıyan atomlar iki yöne saparlar. Sonuç olarak bir atomdaki herbir elektron dört kuantum sayısı; n, l, ml, s ile gösterilebilir ve böylece elektronun bulunduğu yörünge ve dönme yönü belirlenebilir. Fakat elektronların alabileceği kuantum sayılarına ilişkin bir kısıtlama vardır. Bu Pauli İlkesi olarak bilinir. Buna göre; bir atomda, herhangi iki elektronun bütün kuantum sayıları birbirinin aynı olamaz en azından biri farklı olmak zorundadır. örneğin bir yörüngeye ait n, l ve ml değerleri aynı ise bu yörüngeye girecek elektronlardan birinin spini +1/2 ise diğer elektron ancak -1/2 değerini alabilir (Şekil 3). Bu nedenle, herhangi bir yörüngedeki elektron sayısı ancak 2 olabilir demektir. Şekil 4 : Stern-Gerlach Deneyi Elektron spini, atom ve moleküller için gözlenen manyetik özelliklerin açıklanmasına yarar. Üç tür manyetik özellikten söz edilebilir. Bir bileşik, magnetik alan tarafından çekilmez hatta hafifçe iteklenirse bu tür bileşiklerde spini bir yönde olan elektronların sayısı spini diğer yönde olan elektronların sayısına eşit demektir. Bu bileşikler diyamagnetik olarak adlandırılırlar. Magnetik alan tarafından hafifçe çekilen bileşikler ise paramagnetik olarak adlandırılır. Bu tür bileşiklerde spinleri bir yönde olan elektronların sayısı spini diğer yönde olanların sayısından farklıdır. Ferromagnetik maddeler olarak adlandırılan diğer grup ise paramagnetik maddelerden daha güçlü olarak magnetik alandan etkilenirler. Bu maddelerin en önemlisi demirdir. Elektronlar normal şekilde orbitalleri en düşük enerji seviyesindeki orbitallerden başlayarak doldururlar. Bu kural Aufbau İlkesi olarak bilinir. Eş enerjili orbitaller doldurulurken elektronlar orbitallere maksimum toplam spin verecek şekilde yerleşirler. Bu Kural da Hund kuralı olarak bilinir. Şekil 3 : Elektronları orbitallere yerleştirilirken kullanılabilecek bir şablon. Elektronlar atomik orbitalleri doldurdukça kuantum sayılarının durumuna göre atomun özelliklerini de belirlerler. Bu konuya daha ayrıntılı olarak ilerleyen konularda değinilecektir. Atomik orbitallere elektronların yerleştirilmesine yardım edecek pratik bir grafik Şekil 5 de verilmiştir. Herbir orbitale girebilecek elektron sayısı belli olduğundan herhangi bir atom numarası verilecek olursa o atom numarasına sahip atomun elektron konfigürasyonu kolayca yazılabilir. Bir atomun elektron konfigürasyonunu göstermek için alt tabaka simgeleri üzerine içerdikleri elektron sayısı yazılabilir. Tablo 4'de I kolonunda gösterilmiştir. Daha ayrıntılı olarak yörüngeleri kısa çizgi ve spinleri farklı elektronları bunun üzerine aşağı yukarı yönlü okla göstererek yazılabilir. Tablo 4 de II kolonunda gösterilmiştir. Ayrıca Tablo 4, III. kolonda gösterildiği gibi soygaz yapısına bağlı olarak atomların elektron dağılımları gösterilebilir. Daha ayrıntılı bir gösterip Tablo 4 IV. kolonda verilmiştir. Tablo 4 : Atom numarası 1-10 arasındaki atomlar için elektronların orbitalleri doldurmaları. I II III IV \rm _1H : 1s^1 \rm _1H : { \uparrow \over 1s } \rm _2He : 1s^2 \rm _2He : { \uparrow \downarrow \over 1s } \rm _2He : [He] \rm _3Li : 1s^2 2s^1 \rm _3Li : { \uparrow \downarrow \over 1s } { \uparrow \over 2s } \rm _3Li : [He] { \uparrow \over 2s } \rm _4Be : 1s^2 2s^2 \rm _4Be : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s } \rm _4Be : [He] { \uparrow \downarrow \over 2s } \rm _5B : 1s^2 2s^2 2p^1 \rm _5B : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s }{ \uparrow \over 2p} \rm _5B : [He] { \uparrow \downarrow \over 2s }{\uparrow \over 2p} \rm _5B : [He] { \uparrow \downarrow \over 2s }{\uparrow \over 2p_x }{ \over 2p_y} {\over 2p_z} \rm _6C : 1s^2 2s^2 2p^2 \rm _6C : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s }{\uparrow \over \; \;}{\uparrow \over 2p} { \over \; \; } \rm _6C : [He] { \uparrow \downarrow \over 2s }{\uparrow \over \; \;}{\uparrow \over 2p} { \over \; \; } \rm _6C : [He] { \uparrow \downarrow \over 2s }{\uparrow \over 2p_x }{ \uparrow \over 2p_y} {\over 2p_z} \rm _7N : 1s^2 2s^2 2p^3 \rm _7N : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s }{\uparrow \over \; \; }{\uparrow \over 2p} { \uparrow \over \; \; } \rm _7N : [He] { \uparrow \downarrow \over 2s }{\uparrow \over \; \;}{\uparrow \over 2p} { \uparrow \over \; \; } \rm _7N : [He] { \uparrow \downarrow \over 2s }{\uparrow \over 2p_x }{ \uparrow \over 2p_y} { \uparrow \over 2p_z} \rm _8O : 1s^2 2s^2 2p^4 \rm _8O : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over \; \; }{\uparrow \over 2p} { \uparrow \over \; \; } \rm _8O : [He] { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over \; \; }{\uparrow \over 2p} { \uparrow \over \; \; } \rm _8O : [He] { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over 2p_x }{ \uparrow \over 2p_y} { \uparrow \over 2p_z} \rm _9F : 1s^2 2s^2 2p^5 \rm _9F : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over \; \; }{\uparrow \downarrow \over 2p} { \uparrow \over \; \; } \rm _9F : [He] { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over \; \; }{\uparrow \downarrow\over 2p} { \uparrow \over \; \; } \rm _9F : [He] { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over 2p_x }{ \uparrow \downarrow \over 2p_y} { \uparrow \over 2p_z} \rm _{10}Ne : 1s^2 2s^2 2p^6 \rm _{10}Ne : { \uparrow \downarrow \over 1s } { \uparrow \downarrow \over 2s }{\uparrow \downarrow \over \; \; }{\uparrow \downarrow \over 2p} { \uparrow \downarrow\over \; \; } \rm _{10}Ne : [He] { \uparrow \downarrow \over 2s } {\uparrow \downarrow \over \; \; }{\uparrow \downarrow\over 2p} { \uparrow \downarrow \over \; \; } \rm _{10}Ne : [Ne] Bazı atomların elektron dağılımları tam olarak yukarıda anlatılan kurallara uymayabilir. Bunlara örnek olarak 24Cr ve 29Cu dağılımı verilebilir. \rm _{24}Cr : [Ar] { \uparrow \downarrow \over 4s} { \uparrow \over } { \uparrow \over } { \uparrow \over 3d } { \uparrow \over } { \over \; \; } \qquad _{29}Cu : [Ar] { \uparrow \downarrow \over 4s} { \uparrow \downarrow \over } { \uparrow \downarrow \over } { \uparrow \downarrow \over 3d } { \uparrow \downarrow \over } { \uparrow \over \; \; } fakat yapılan deneysel çalışmalar ile yapılarının; \rm _{24}Cr : [Ar] { \uparrow \over 4s} { \uparrow \over } { \uparrow \over } { \uparrow \over 3d } { \uparrow \over } { \uparrow \over \; \; } \qquad _{29}Cu : [Ar] { \uparrow \over 4s} { \uparrow \downarrow \over } { \uparrow \downarrow \over } { \uparrow \downarrow \over 3d } { \uparrow \downarrow \over } { \uparrow \downarrow \over \; \; } şeklinde olduğu bulunmuştur. Bu Jahn-Teller Etkisi olarak adlandırılır. Buna göre; Eğer elektronlar dejenere enerji seviyelerini tam olarak dolduramazlarsa, asimetrikliğin giderileren daha kararlı hale gelmek için dejenere olmayan enerji seviyelerindeki elektronlar kullanırlar ve daha kararlı hale gelirler. Elektron vermiş (iyonlaşmış) elementlerin elektron dizilişleri için Şekil 3 deki enerji düzeyleri şeması kullanmak yanlışlığa yol açabilir. Örneğin demir atomunun iyonlaşması sonucu oluşacak elektron dağılımı; \rm _{26}Fe : 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 3d^6 \rm _{26}Fe : 1s^2 2s^2 2p^6 3s^2 3p^6 3d^6 4s^2 \rm _{26}Fe^{+2} : 1s^2 2s^2 2p^6 3s^2 3p^6 3d^6 şeklindedir. Buradan da görüldüğü gibi iyonlaşma sonucu 3d elektronları değil 4s elektronları atomdan uzaklaşmıştır. Gerçekte de 3d elektronları ortalama olarak çekirdeğe 4s elektronlarından daha yakındırlar. Bu nedenle 4s elektronları daha kolay verilirler. Kural olarak; iyonlaşma ile verilen elektronlar n sayısı en büyük olan elektronlardır. Bundan dolayı elementlerin elektron dizilişlerini enerji düzeyleri şemasına göre yazdıktan sonra alt tabakları artan n sayısına göre düzenleyerek yeniden yazmak daha uygun olabilir. Örneğin 53I ve 53I- için; \rm _{53}I : 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 3d^{10} 4p^6 5s^2 4d^{10} 5p^5 \rm _{53}I : 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 3d^{10} 4p^6 4d^{10} 5s^2 5p^5 \rm _{53}I : [Kr] 4d^{10} 5s^2 5p^5 \rm _{53}I^- : [Kr] 4d^{10} 5s^2 5p^6 Ayrıca \rm _{53}I^- : [Kr] 4d^{10} 5s^2 5p^6 \rm _{53}I^- : [Xe] Aynı elektron dizilişine sahip veya iyonlar izoelektronik olarak adlandırılırlar. Bu nedenle 53I- ve Xe izoelektroniktirler.