Serbest Enerjinin Sıcaklığa Bağımlılığı ve Reaksiyon Denge SabitiBu kısımda denge sabitinin sıcaklıkla nasıl değiştiğini serbest enerji değişimlerine bağlı olarak hesaplamamıza yardım edecek eşitlikleri elde etmeye çalışacağız. \rm \Big( { \partial G \over \partial T } \Big)_P=-S
eşitliğine göre, bir reaksiyonda yer alan herhangi bir bileşiğin serbest enerjisi sıcaklığa bağımlıdır. Yukarıdaki eşitliği kimyasal bir reaksiyon için \rm \Big( { \partial \Delta G \over \partial T } \Big)_P=- \Delta S
şeklinde yazabiliriz. Burada \rm \Delta G= G_{ürünler} - G_{reaktifler} ve \rm \Delta S= S_{ürünler} - S_{reaktifler} dir. Herhangi bir sabit sıcaklıktaki kimyasal reaksiyon için serbest enerjinin entalpi ve entropiye bağımlılığı \rm \Delta G = \Delta H - T \Delta S
\rm
\Delta S={ \Delta H - \Delta G \over T } \quad (T=sabit) \qquad \qquad (I)
eşitliği ile verilebileceğini daha önce görmüştük. İkinci eşitlik \rm \Delta S teriminden kurtulmak için kullanılabilir. \rm \Big( { \partial \Delta G \over \partial T } \Big)_P= - { \Delta H \over T } +{ \Delta G \over T }
ya da \rm \Big( { \partial \Delta G \over \partial T } \Big)_P - { \Delta G \over T } = - { \Delta H \over T }
Eşitliğin solundaki terim ; \rm
\Big[ { \partial \over \partial T } \Big( { \Delta G \over T } \Big) \Big]_P =
{ 1 \over T } \Big( { \partial \Delta G \over \partial T } \Big)_P + G { d \over dT } { 1 \over T }
\rm
\qquad \qquad \qquad =
{ 1 \over T } \Big( { \partial \Delta G \over \partial T } \Big)_P - { G \over T^2 }
\rm
\qquad \qquad \qquad =
{ 1 \over T } \Big[ \Big( { \partial \Delta G \over \partial T } \Big)_P - { \Delta G \over T } \Big]
şeklinde basitleştirilebilir. Bu basitleştirilmiş eşitlik ile Eşitlik (I) birleştirilse \rm
\Big[ { \partial \over \partial T} \Big( { \Delta G \over T } \Big) \Big]_P =- { \Delta H \over T^2}
ya da \rm
T \Big[ { \partial \over \partial T} \Big( { \Delta G \over T } \Big) \Big]_P =- { \Delta H \over T}
eşitliği elde edilir. Bu eşitliğe Gibbs-Helmholtz Eşitliği denir. Standart haldeki basınç ve sıcaklıkta \rm
T \Big[ { \partial \over \partial T} \Big( { \Delta G^o \over T } \Big) \Big]_P =- { \Delta H^o \over T}
yazılabilir. Sonuç olarak \rm \Delta G^o ile denge sabiti arasındaki ilişki daha önce elde edilmiş olan serbest enerji-denge sabiti ilişkisi kullanılarak;
\rm { d(lnK) \over dT } = { \Delta H^o \over RT^2 }
\rm \int d(lnK) = { \Delta H^o \over R } \int { dT\over T^2}
\rm lnK = -{ \Delta H^o \over R } { 1\over T} + Sabit
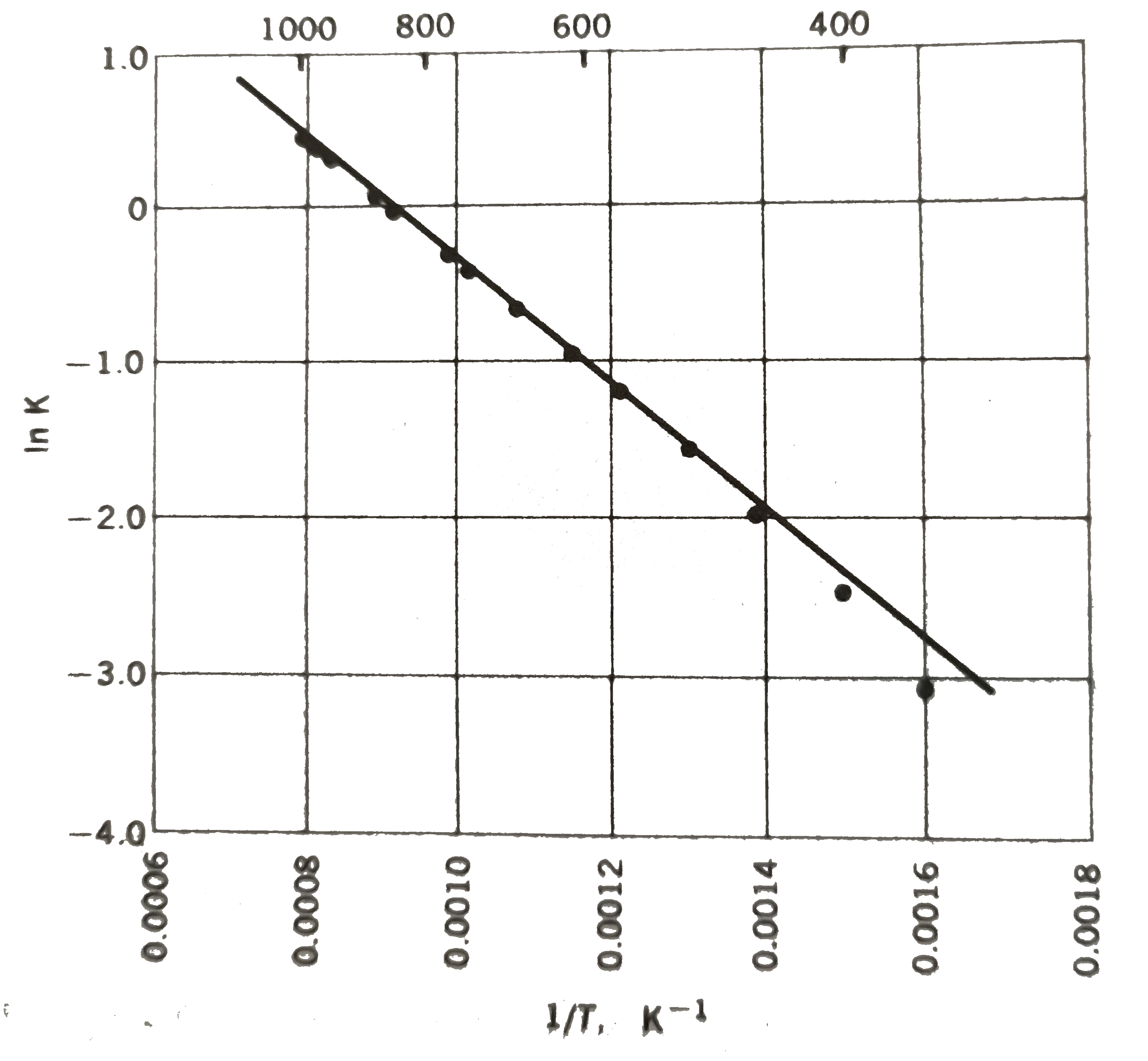
\rm {1 \over T }\text{ ye karşı } lnK \text{ grafiğinin eğimi } -{ \Delta H^o \over R } \text{değerini verir. )} \rm \int _{ K_1 } ^{ K_2 } d(lnK) = { \Delta H^o \over R } \int _{ T_1} ^{T_2} { dT\over T^2}
\rm ln { K_2 \over K_1} = -{ \Delta H^o \over R } \Big( {1 \over T_2} - {1 \over T_1} \Big)
\rm \text{iki farklı sıcaklık için bilinen K değerlerinden } \Delta H^o \text{ hesaplanabilir. } şeklinde elde edilebilir. Bu eşitliğin türevin sonucudur. Sıcaklık ile denge sabitinin değişmesi reaksiyon standart ısısına bağlıdır. Şekil 1 de \rm CO_2 \; ve \; H_2 arasındaki denge reaksiyonu için sıcaklık ile denge sabitinin değişimi görülmektedir.
Büyük sıcaklık aralıkları düşünülürse, sıcaklığa denge sabitinin bağımlılığı ile ilgili olarak \rm \Delta G^o = \Delta H^o - T \Delta S^o
\rm \Delta G^o = -RT lnK
eşitlikleri dikate alınarak \rm -RT lnK = \Delta H^o - T \Delta S^o
eşitliği yazılabilir. Bu eşitliğe göre herhangi bir sıcaklık için denge sabitinin \rm \Delta H^o \; ve -T \Delta S terimlerine bağlı olarak değiştiği görülmektedir. Şekil 2 de reaksiyon termodinamik parametrelerinin sıcaklık ile nasıl değiştiği görülmektedir. Şekilde de görüldüğü gibi entopinin pozitif veya negatif olmasının denge sabiti üzerine açık etkisi görülmektedir.
|