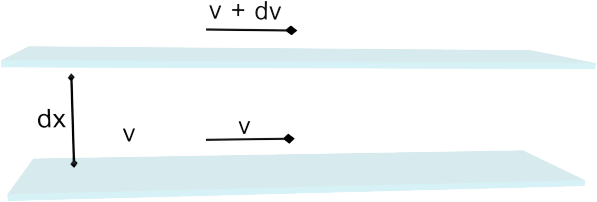Sıvılarda Akmaya Karşı Direnç : ViskoziteSıvının içindeki içsel sürtünme kuvvetinin bir sonucu olarak sıvı akmaya karşı bir direnç oluşturur. Daha yüksek viskoziteye sahip sıvılar, daha yüksek sürtünme kuvvetlerine sahiptir ve dolayısıyla daha yavaş akarlar. Bu konuya madde veye enerjinin taşınımı konusu üzerindeyken durmuştuk. Şimdi tabakalar arasındaki etkileşmeyi daha ayrıntılı olarak inceleyelim.
Şekil 1 de görüldüğü gibi bir akışkan içinde tabakalar bulunduğunu ve bu tabakaların birbirlerine etkileyerek akmaya karşı bir dienç oluşturduğunu düşünelim., Akışkan içindeki bir tabakanın kendisine komşu tabakanın hareketine karşı gösterdiği sürtünme kuvveti; F, tabakanın alanı; A, ve hız gradiyenti; \rm dv \over dx , ile doğru orantılı olarak \rm F= \eta A { dv \over dx } \qquad \qquad \qquad (Eşitlik \; 1 )
eşitliği ile verilir. Burada \rm \eta ; bir orantı kaysayısı olup viskozite katsayısı veya s adece viskozite olarak adlandırılır. Viskozitenin tersine akışkanlık, \rm \phi denir ( \rm \phi = {1 \over \eta }). Viskozite katsayısının SI birimi daha önce bahsettiğimiz gibi \rm kg \; m^{-1} \; s^{-1} veya \rm kg \; N \; s m^{-2} dir. Bununla beraber sık olarak SI birim onda biri olan poise ( \rm g \; cm^{-1} \; s^{-1} ) birimi kullanılmaktadır. Bir sıvının akışını ölçmek için kullanılan yöntemler
olarak sıralanabilir.
Kütle Akış Ölçümleri (Kapiler Akma Yöntemi) : Bastırılamayan bir akışkanın r yarıçaplı ve L uzunluğundaki bir boru içinde akarken, sıvının bir ucundaki basınç \rm P_1 diğer ucundaki basıncın \rm P_2 olduğunu varsayalım. Borunun iç yüzeyine bitişik sıvı tabakası hareketsiz iken, akış hızı borunun merkezinde maksimumdur. Uzunluğu L ve yarıçapı r olan bu silindirik borunun iç yan yüzünün alanı \rm 2 \pi r L dir. Eşitlik 1 'e göre sürtünme kuvveti \rm F= \eta A { dv \over dx } = - \eta 2 \pi r L { dv \over dr } \qquad \qquad \qquad (Eşitlik \; 2 )
yazılır. Burada hız gradienti olan, \rm { dv \over dr }, negatif değerlidir. Çünkü merkezden duvara gidildikçe, yani r arttıkça akış hızı azalır. F sürtünme kuvveti, silindirdeki akışkanı yürüten kuvvet tarafından tam olarak dengelenir. Bu yürütücü kuvvet, basınç farkının ( \rm P_1 - P_2) silindirin taban alanı, \rm \pi r^2, ile çarpımına eşittir. \rm - \eta 2 \pi r L { dv \over dr } = \pi r^2 (P_1 -P_2)\qquad \qquad \qquad (Eşitlik \; 3 )
\rm \int _o ^v dv = - \int _R ^r { \pi (P_1-P_2) \over 4 \eta L } dr \qquad \qquad \qquad (Eşitlik \; 4 )
\rm v = { (P_1-P_2) \over 4 \eta L } \big( R^2 -r^2 \big) \qquad \qquad \qquad (Eşitlik \; 5 )
Birim zaman da akan toplam sıvı hacmi \rm dV \over dt kesit alanın herbir elemanı için integre edilerek elde edilir. \rm { dV \over dt } = \int _o ^R 2 \pi rvdr
\rm { dV \over dt } = { (P_1-P_2) \pi \over 2 \eta L } \Big( R^2 \int _o ^R rdr - \int _o ^R r^3dr \Big)
\rm { dV \over dt } = { (P_1-P_2) \pi R^4 \over 8 \eta L } \qquad \qquad \qquad (Eşitlik \; 6 )
Eşitlik 6 Poiseuille Eşitliği olarak bilinir. ve basınç farkı biliniyorsa boyutları bilinen borudaki akış hızının ölçülmesi ile \rm \eta hesaplanabilir. Akışa neden olan basınç farkı, \rm P_1-P_2, sıvının yoğunluğu, \rm \rho , boru veya kapilerin uzunluğu, L, ve deneyin yapıldığı yerdeki yerçekim ivmesi, g, olmak üzere \rm P_1-P_2 = \rho g L
şeklinde yazılabilir. Eşitlik 6 Böylece
\rm { dV \over dt } = { \rho g L \pi R^4 \over 8 \eta } \qquad \qquad \qquad (Eşitlik \; 7 )
Eşitlik 7 t=0 ve V=0 başlangıç şartı ile integrali alınırsa \rm \eta = { \pi R^4 g \over 8 V L } \rho t \qquad \qquad \qquad (Eşitlik \; 8 )
eşitliği elde edilir. Bu eşitlikteki büyüklükleri ayrı ayrı belirlemek güç olabileceğinden, aynı viskozimetre ile aynı hacimdeki sıvıların akma sürelerini ölçmek daha pratik bür yoldur. Eşitlik 8 iki sıvı için ayrı ayrı yazılır ve oranlanırsa \rm { \eta _{ örnek } \over \eta _{ referans } } = { \rho _{örnek} t _{örnek} \over \rho _{referans} t _{referans} } \qquad \qquad \qquad (Eşitlik \; 9 )
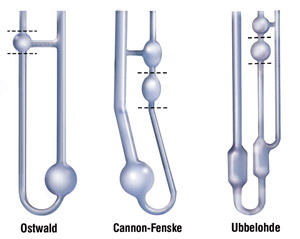
eşitliğinden kolayca hesaplanabilir. Şekil 2 bu amaçla kullanılan bazı viskozimetre çeşitleri görülmektedir. Düşen Küre Yöntemi : Yarıçapı, r, yoğunluğu \rm \rho olan küresel bir cisme, yoğunluğu \rm \rho _{s} olan bir sıvı içerisinde yerçekimi ivmesi g olan bir yerdeki yerçekim kuvveti \rm F_g= { 4\over 3} \pi r^3 \big( \rho - \rho _ {s} \big) g \qquad \qquad \qquad (Eşitlik \; 10 )
ile verilir. Küre bu kuvvet etkisi altında hızlanır. Sıvı içinde hareket eden küreye etki eden sürtünme kuvveti ise kürenin hızının artışı ile artar. Sonunda küre v limit bir hızına ulaşır. Stokes bu durumdaki küresel cismin karşılaştıüı sürtünme kuvvetinin \rm F_{ sürtünme} = 6 \pi r \eta v \qquad \qquad \qquad (Eşitlik \; 11 )
şeklinde olduğunu göstermiştir. Eşitlik 10 ve Eşitlik 11 deki iki kuvvet eşitlendiğinde viskozite katsayısı \rm \eta; \rm \eta = { 2r^2 \big( \rho - \rho _ {s} \big) g \over 9 v} \qquad \qquad \qquad (Eşitlik \; 12 )
olarak elde edilebilir. Küre limit hıza ulaştığında L uzunluğunu t zamanında almışsa limit hız v; \rm v = { L/t } olacağından \rm \eta = { 2r^2 \big( \rho - \rho _ {s} \big) g t\over 9 L } \qquad \qquad \qquad (Eşitlik \; 13 )
eşitliği yazılabilir. Eğer \rm \rho < \rho _ {s} ise; bilye sıvı içinde düşmek yerine yüzeye doğru yükselecektir. Sıvıda çözünmeyen küresel bir kabarcığın yükselmesi kullanılarak sıvının viskozitesi bu yöntem ile ölçülebilir. Sıvıların Viskozitesi Üzerine Sıcaklığın Etkisi : Sıvıların viskozitesi genel olarak sıcaklık artışı ile azalır. Bu sıcaklık artması ile tabakalar arasındaki moleküler geçişlere bağlı olarak açıklanabilir. Ancak bazı polimerik sıvılarda sıcaklık artışı ile viskozitede artabilir. Bunun nedeni sıcaklık artışı ile polimerik moleküllerin daha geniş yüzey alanına veya hacme sahip olarak hareket etmelerinin bir sonucudur. Genel olarak viskozitenin sıcaklık ile değişimi \rm \eta = A e^{ E_v \over RT} \qquad \qquad \qquad (Eşitlik \; 14 )
eşitliği ile verilir. Burada A sabit bir sayı \rm E_v ; viskozite aktivasyon enerjisidir. \rm 1 \over T yer karşı \rm ln \eta grafik edilerek elde edilen doğru denkleminden A ve \rm E_v değeri hesaplanabilir. Tablo 1 de bazı sıvıları sıcaklık ile viskozite katsayılarının değişimi görülmektedir.
Çözeltilerde Viskozite : Çözeltilerin viskozitesi sabit sıcaklık ve basınçta, konsantrasyona bağlı olarak ve çözünen türün doğasına bağlı olarak artar veya azalabilir. Bazı maddelerin çeşitli konsantrasyonlardaki viskozite büyüklükleri Tablo 2 de verilmiştir. Tablodan da görüldüğü gibi bazı çözeltilerin viskozitesi konsantrasyon artışı ile artarken bazı çözeltilerin düşmektedir. Ancak genel olarak konsantrasyon artışı ile viskozitenin arttığı söylenebilir.
Einstein Bağıntısı yardımı ile çözeltinin viskozite büyüklüğü, \rm \eta _1, ve saf çözücünün viskozite büyüklüğü, \rm \eta _o, olmak üzere \rm \eta _1 = \eta _o (1+2.5 \phi) \qquad \qquad \qquad (Eşitlik \; 15 )
bağıntısı verilir. Burada \rm \phi ; çözeltinin birim hacminde çözünmüş madde miktarının hacmini belirler. Bu bağıntı küresel partiküller yapı dikkate alınarak çıkartılmıştır. Ancak partiküller kürsellikten saptıklarında Eşitlik 15 de yar alan 2.5 sabit değeri de değişir. Bu değer \rm \nu ile gösterilir. Bu değerin değişimi elipsoidal şeklindeki taneciklerin c/a=e ( boy/en )oranına bağlı olarak alabileceği değerler aşağıdaki Tablo 3 de gösterilmiştir.
Kaynaklar
|