Taşınım Özellikleri

Bir maddenin taşınım özelliği; maddenin, enerjinin veya bazı diğer özelliklerinin bir yerden bir başka yere taşınması kabiliyetidir. Örneğin, Gazlardaki, sıvılardaki veya katılardaki moleküller bileşimleri aynı oluncaya kadar derişimlerini azaltacak şekilde yayılma eğilimindedirler. Yayılma hızı bir taşınım özelliğidir. Termal iletim hızı; termal enerjinin daha düşük sıcaklığa akma eğilimidir. Elektriksel iletkenlik, bir potansiyeldeki yüklerin (iyon veya elektron) taşınmasıdır ve bir maddenin elektriksel iletkenliği taşınım özelliğidir. Viskozite (akmazlık) bir sıvı boyunca lineer momentumun hızının ölçülmesidir ve bu nedenle bir başka taşınım özelliği olarak karşımıza çıkar. Bu kısımda genel anlamda taşınım olayını ile ilgileneceğiz ve sonra gazların kinetik teorisini kullanarak taşınım özelliklerinin bazılarını hesaplayacağız. Akış Akış J ile gösterilen bir özelliğin göç hızı, bir özelliğin birim alan boyunca ilerlemesinin ölçülmesiyle elde edilir. Eğer akan kütle ise (diffüzyonda olduğu gibi), kütle akışı olarak söylenir ve birimi çoğu zaman kg m-2 s-1 olarak verilir. Özellik enerji ise (termal iletkenlikte olduğu gibi), enerji akışı olarak söylenir ve birimi çoğu kez J m-2 s-1 dir. Diğer özellikler için benzer şeyler söylenebilir. Taşınım özellikleri üzerindeki yapılan deneysel gözlemler, bir özelliğin akışının genellikle bir sistemdeki ilişkin özelliğin gradineti ile orantılı olduğunu göstermiştir. Örneğin; z eksenine parelel olarak düffüzlenen madde akışı (Jz) eksendeki konsantrasyon gradineti ile orantılıdır. 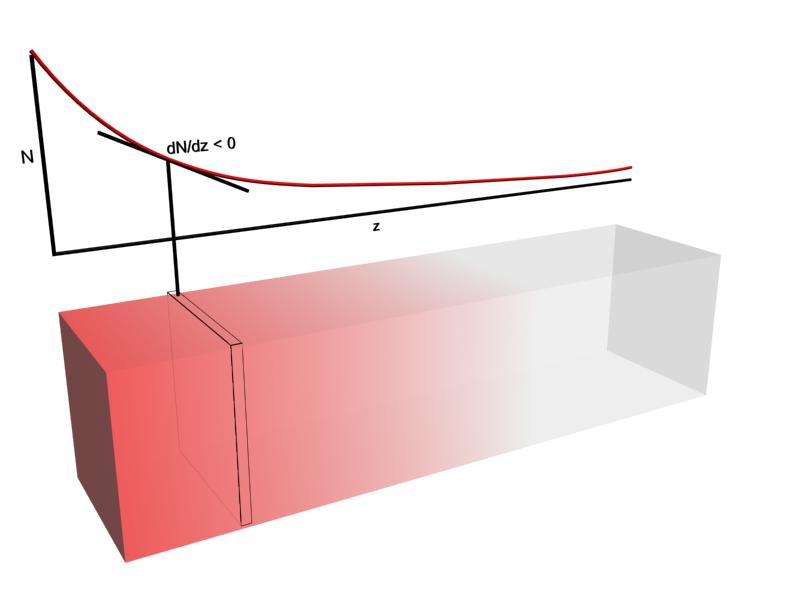Şekil 1 : Maddenin yayılması ile konsantrasyon değişimi. dN/dz < 0 dir. \rm J_{z}(madde) \quad \alpha \quad { dN \over dz } Madde akışının konsantrasyon gradienti ile orantılılığı diffüzyon için Birinci Fick Yasası olarak adlandırılır. Benzer şekilde termal diffüzyon hızı (termal hareketin enerji akışı) sıcaklık gradineti ile orantılıdır. \rm J_{z}(enerji) \quad \alpha \quad { dT \over dz } Akış Jz bir vektör bileşenidir. Eğer Jz > 0 ise; akış sağa doğru artar. Eğer Jz < 0 ise; akış sola doğru artar. Konsantrasyon sağa doğru azalıyor ise; dN/dz < 0 dır ve Jz pozitiftir (akış sağa doğrudur.). Bu nedenle, madde akış eşitliğindeki orantı katsayısı negatif olmalı ve -D ile gösterilir. Buradaki D, sabiti diffüzyon katsayısıdır. Böylece \rm J_{z}(madde) = -D { dN \over dz } Termal hareket enerjisi sıcaklık gradientinin altına düşer ve benzer şekilde \rm J_{z}(enerji) = - \kappa { dT \over dz } yazılır. Buradaki k; termal iletkenlik katsayısıdır. Şekil 2 : Akışkanın ince tabakalar halinde hareketi. Momentumun akışı ve viskozite arasındaki ilişkiyi görmek için, newtonian akış halindeki bir akışkanı göz önünde bulundurmalıyız. Akışkanın ince tabakalar halinde aktığı düşünülebilir. Kabın duvarına bitişik tabaka yakınındaki tabaka hareketsidir ve ardından gelen tabakaların hızları duvardan uzaklaştıkça doğrusal olarak değişir. Moleküller devamlı olarak tabakalar arasında hareket eder ve bulundukları tabakadan momentumun x bileşenini getirirler. Tabaka, soldan gelen bir molekül tarafından yavaşlatılır. Çünkü bu moleküller düşük momentuma sahiptirler. Tabaka, sağdan gelen bir molekül tarafından hızlandırılır. Çünkü bu moleküler yüksek momentuma sahiptirler. Bu nedenle hızlı tabakalar, moleküllerin ulaşmaları ile yavaşlatılırken, yavaş tabakalar hızlanırlar. Tabakalar aynı hızda olma eğilimindedirler. Hızlı tabakalar üzerine yavaş tabakaların geciktirme etkisini akışkan viskozitesi olarak açıklayabiliriz. Böylece, Viskozite z-yönündeki x-momentumunun akışına bağımlı olarak karşımıza çıkar. x-momentumunun akışı dvx/dz ile orantılıdır. Çünkü, tüm tabakalar aynı hızla hareket ederlerse hiçbir akış meydana gelmiyor demektir. Böylece \rm J_{z}(x \;boyunca \;momentum) \quad \alpha \quad { d \nu_{x} \over dz } veya \rm J_{z} = - \eta \big( { d \nu_{x} \over dz } \big) yazılabilir. Buradaki \rm \eta ; viskozite katsayısıdır (veya basitçe viskozitedir.). Taşınım Katsayısının Birimi \rm \eta h nın birimi, son eşitlikten elde edilebilir. Momentum akışı, [momentum][alan]-1[zaman]-1 boyutuna sahiptir. \rm akış = ( kg. \; m. \; s^{-1})(m.^{-2})(s^{-1}) = kg. \; m^{-1} \; s^{-2} Hız gradientinin boyutları [hız][uzunluk]-1 olduğundan, \rm [Hız \; Gradienti] = ( m. \; s^{-1})(m.^{-1}) = s^{-1} Böylece \rm [Viskozite] = kg. \; m.^{-1} \; s^{-1} olarak elde edilebilir. Viskoziteler genellikle poise (P) olarak verilir. 1 P = 10-1 kg m-1 s-1 dir. Gazların Viskozite Büyüklüğü Gazların viskozitesi küçük olduğundan gazların viskozitesi için poise birimi yerine mikropoise ( \rm 1 \; P \; = 1 \times 10^6 \; \mu P ) birimi tercih edilir. sıvıların viskozitesi genellikle santipoise (10-2 P) büyüklüğü ile verilir. Sıvıların viskozitesi sıcaklık artışı ile azalırken, gazların viskoziteleri sıcaklık artışı ile artar. Gazların sıcaklık artışı ile viskozitelerinin artma nedeni moleküler arası çarpışmaların sayısının artmasından kaynaklanır. Gazların viskozite katsayısı; gaz moleküllerinin ortalama hızları, \rm \overline{u}, ortalama serbest yol uzunlukları, L ve yoğunlukları, d ye bağlı olarak \rm \eta = {1 \over 3} \overline{u} L d \qquad \qquad \qquad (1) eşitliği ile verilir.