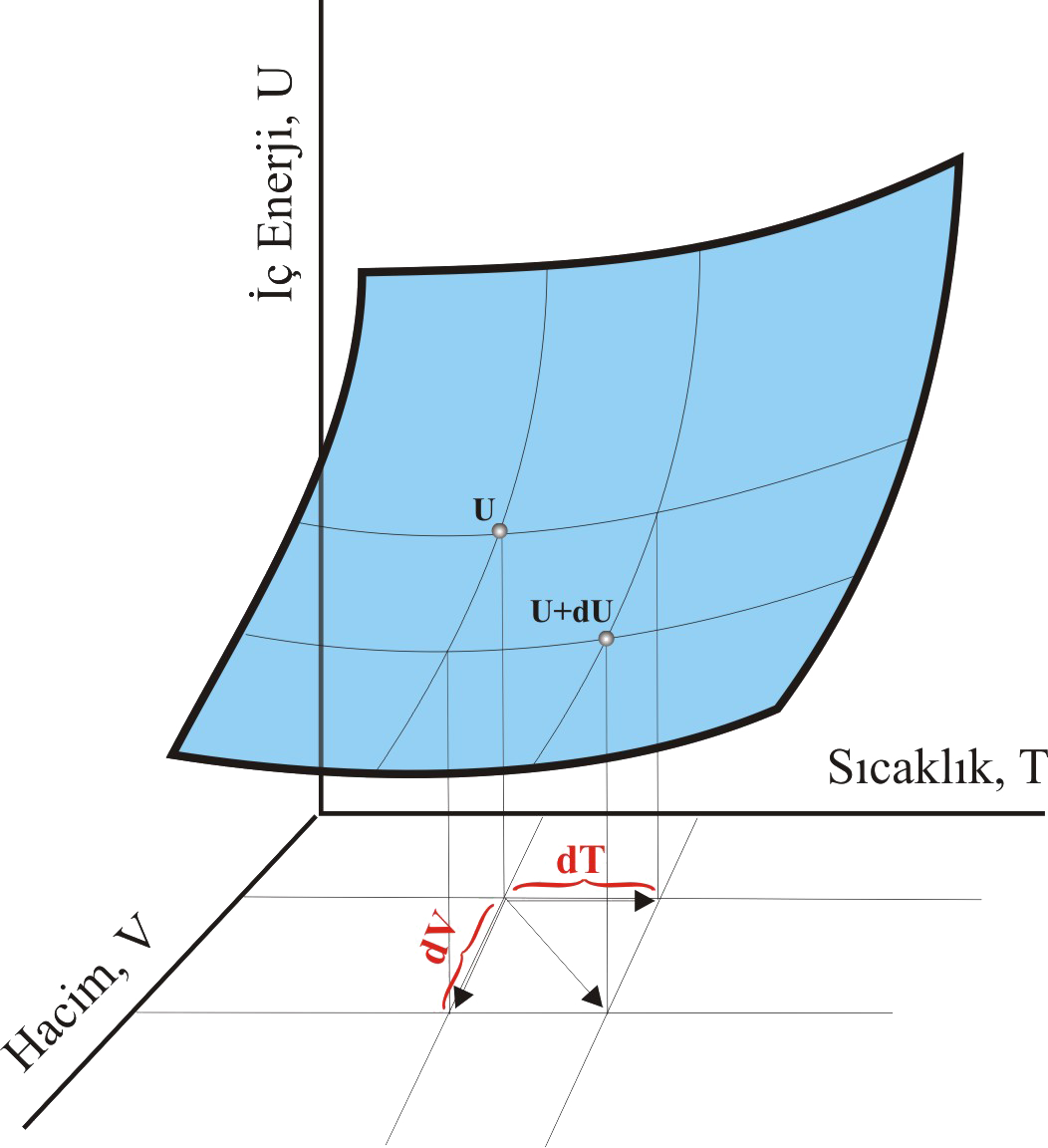
İç Enerji Değişimleriİç enerji, P, V, T lığın bir fonksiyonu olarak ele alınabilir. Ancak bu değişkenlerden ikisi biliyorsa, üçüncüsü bilineceğinden ikisinin seçilmesi yeterlidir. Bu nedenle İç enerji 2 değişkenin değişimine bağlı olarak yazılabilir.
İç enerji değişimi hacim ve sıcaklık değişiminin bir fonksiyonu olarak \rm dU =
\big( { \partial U \over \partial V} \big)_T dV
+
\big( { \partial U \over \partial T} \big)_V dT
\qquad \qquad \qquad (1)
şeklinde yazılabilir. Bu denklem sabit bileşimli kapalı bir sistemde iç enerjideki sonsuz küçük değişimin; hacim ve sıcaklıktaki sonsuz küçük değişikliklerle orantılı ve orantı katsayılarının iki kısmi türevi şeklinde olduğunu gösterir. Eşitlikteki \rm \big( { \partial U \over \partial T} \big)_V dT kısmına karşı gelen katsayı sabit hacimdeki ısı kapasitesi Cv dir. \rm \big( { \partial U \over \partial V} \big)_T dV katsayısı ise hacim değişimi ile iç enerjinin değişiminde rol alır. \rm \pi _T basunç ile aynı boyuta sahip olduğundan ve moleküller arası etkileşimlerin bir sonucu olduğudan iç basınç olarak adlandırılır. Böylece Eşitlik (1) \rm dU =
\pi _T dV
+
C_v dT
\qquad \qquad \qquad (2)
şeklinde yazılabilir. Eğer \rm \pi _T = 0 ise iç enerji değişiminin hacim değişiminden bağımsız olduğunu ve moleküller arası etkileşim ile ilgili bir iç basıncın olmaması anlamını taşır. Bu davranış ideal gaz davranışıdır. Gerçek gazların davranışlarına teorik yaklaşımlardan van der Wall denklemini incelerken, basınç düzeltme faktörü a terimini kullanmıştık. \rm \pi _T = 0 olması demek bu terimin sıfır olduğu anlamına gelir. Eğer \rm \pi _T > 0 ise \rm \pi _T van der Walls denklemindeki basınç düzeltme faktörü \rm n^2a/V^2 karşı gelir ( \rm \pi_T = n^2a/V^2 ). Sistemin hacmi yerine basıncı sabit tutulduğunda iç enerjinin sıcaklık ile nasıl değiştiğini bulmak için Eşitlik (2) nin sıcaklığa göre değişimi için; \rm \big( { \partial U \over \partial T } \big)_P =
\pi _T \big( { \partial V \over \partial T } \big)_P
+
C_v
\qquad \qquad \qquad (3)
şeklinde yazılabilir. Eşitliğin sağ tarafındaki kısmi türev sabit basınçta sıcaklığa karşı hacim değişimi için eğimi gösterir. Bu özellik maddenin genleşme katsayısı olarak \rm \alpha = { 1 \over V }\big( { \partial V \over \partial T } \big)_P
\qquad \qquad \qquad (4)
şeklinde tanımlanır. İzotermal bastırılabilirlik katsayısı ise \rm \kappa = -{ 1 \over V }\big( { \partial V \over \partial P } \big)_T
\qquad \qquad \qquad (5)
eşitliği ile verilir. Madde baskı uygulandığında hacim azalması meydana gelir. Eşitlikteki negatif işareti ile bastırılabilirlik katsayısı pozitif olarak elde edilir. Bazı maddelere ilişkin genleşme katsayıları ve izotermal bastırılabilirlik katsayıları Tablo 1 de verilmiştir.
|