Moleküler Hız Dağılımları

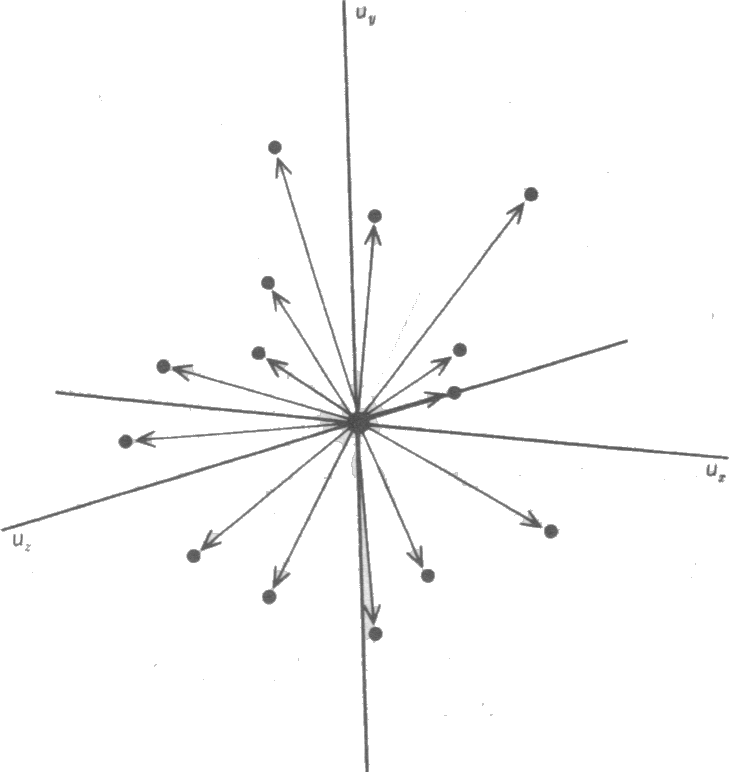
Bir Boyutta Moleküler Hız Dağılımı Çeşitli hız ve enerjilere sahip moleküllerin sayısına ilişkin temel eşitlik Boltzmann Dağılımı ile verilir. Kinetik moleküler teori temel alan modele göre; gaz molekülleri çeşitli hızlarla ve çeşitli yönlere doğru hareket eder. Bu hızlar Şekil 1 de gösterilmiştir. Şekildeki herbir noktanın orjinden uzaklığı moleküler hızın büyüklüğü ile orantılıdır ve tüm yönlere doğru moleküler hızların dağılımı aynı olduğundan izotropik bir davranış gösterir. Şekil 1 : Gaz içindeki moleküllerin vektörel olarak sembolik hız dağılımı. Özel bir yöne doğru örneğin x yönündeki hız dağılımını araştırabiliriz. Eğer ux ile ux+dx hız aralığındaki moleküllerin dN/N kesrini bulmalıyız. Şekilde öne doğru hareket eden moleküllerin ux hızları pozitifken zıt yöne hareket eden moleküllerin hızları ise negatiftir. Bu hız aralığındaki moleküllerin kesri için; \rm {dN \over N} = Ae^{- { 1 \over 2}mu_x^2/kT }du_x kullanılır. Buradaki A orantı sabitidir. Bu sabitin değeri, eşitliğin sağ tarafının integralininden hareketle hesaplanabilir. ux hızının her iki yöndeki tüm olasılıkları \rm u_x = \rm \pm \infty arasında yer alacaktır. Bu nedenle bu hız aralığında dN/N değeri 1 olacaktır. \rm \int_{- \infty}^{+ \infty} Ae^{- { 1 \over 2}mu_x^2/kT }du_x = 1 böylece hız sabiti için; Şekil 2 : 298 ve 1500 K de N2 moleküllerinin bir boyutta hız dağılımı. . \rm A = { 1 \over \int_{- \infty}^{+ \infty} Ae^{- { 1 \over 2}mu_x^2/kT }du_x } yazılabilir. Bu eşitlikten A nın değeri \rm A = \sqrt {m \over 2 \pi k T} olarak hesaplanabilir. 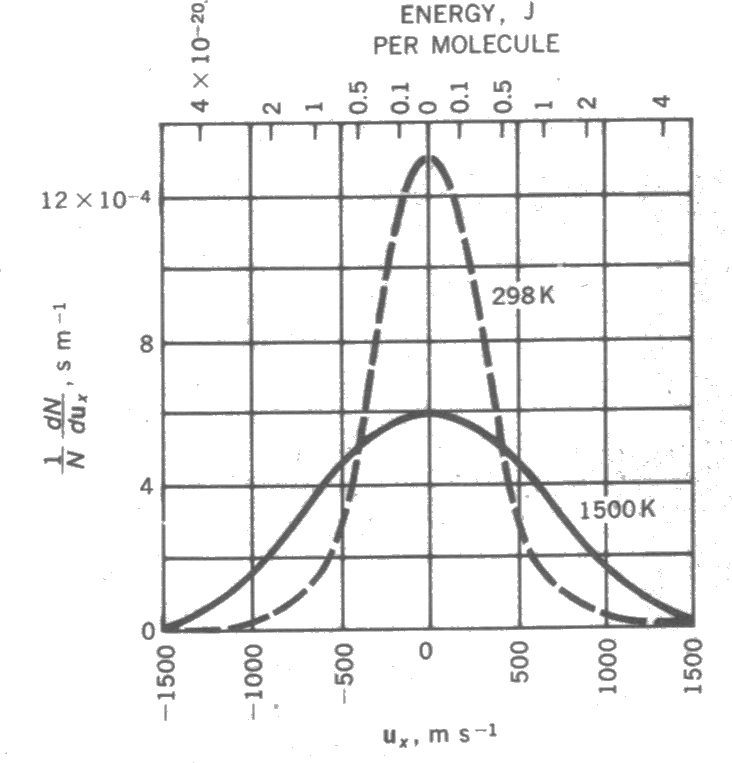Sonuçta N molekülün x yönündeki hız dağılımına ilişkin \rm {dN/N \over du_x} = \sqrt {m \over 2 \pi k T} e^{- { 1 \over 2}mu_x^2/kT } yazılabilir. Şekil 2 de azotun iki farklı sıcaklıktaki bir boyuttaki moleküler hız dağılımı verilmiştir. Üç Boyutta Moleküler Hız Dağılımı Üç boyuttaki hız dağılımı için bir boyuttaki hız dağılımına benzer şekilde moleküllerin x, y ve z doğrultularındaki hız kesirlerini bulabilmek için \rm u_x - u_x+dx, \rm u_y - u_y+dy ve \rm u_z - u_z+dz hız aralığındaki molekülleri dikkate almalıyız. 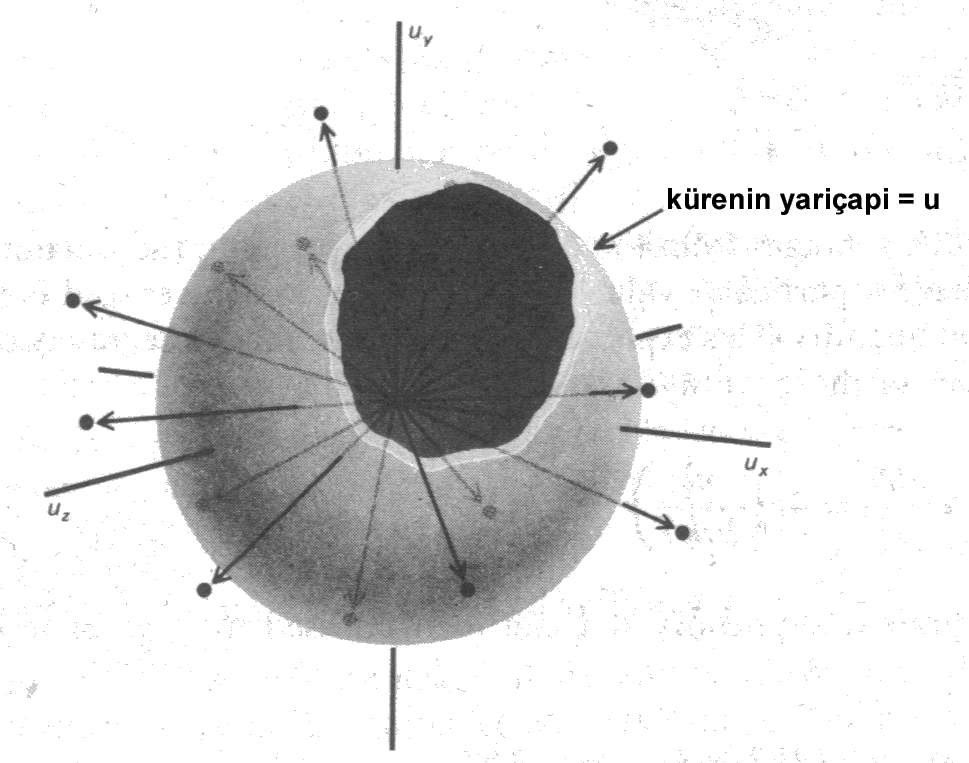Bu nedenle; \rm {dN \over N} = \Big( \sqrt {m \over 2 \pi k T} e^{- { 1 \over 2}mu_x^2/kT }dx \Big) \Big( \sqrt {m \over 2 \pi k T} e^{- { 1 \over 2}mu_y^2/kT }dy \Big) \Big( \sqrt {m \over 2 \pi k T} e^{- { 1 \over 2}mu_z^2/kT }dz \Big) veya \rm {dN/N \over dxdydz} = \Big( {m \over 2 \pi k T} \Big)^{3/2}e^{- { 1 \over 2}m(u_x^2+u_y^2+u_z^2)/kT } yazılabilir. Şekil 3 deki gibi bir hacim elemanı içerisindeki moleküler noktaların yoğunluğunu belirleyebiliriz. Bunlar u hızına sahip moleküllerdir. Çünkü bu küresel kabuğun hacmi \rm 4 \pi u^2 du kadar olup bu elementteki noktaların sayısı yukarıdaki eşitliğin \rm 4 \pi u^2 du \over dxdydz ile çarpılmasıyla elde edilir. Burada \rm u^2 = u_x^2 + u_y^2 + u_z^2 değişimi yapılırsa üç boyutlu hız dağılımı için Şekil 3 : Moleküllerinin üç boyutta (x, y, z) hız dağılımı. 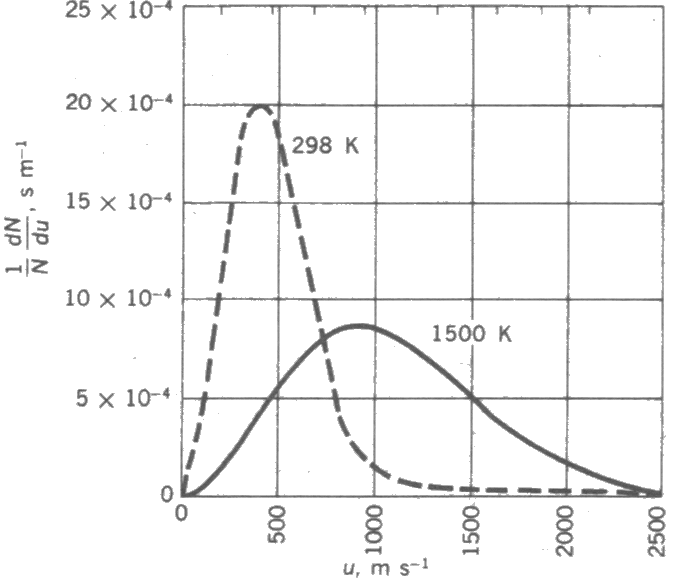\rm P_u = {dN/N \over du} = 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} u^2 e^{- { 1 \over 2}mu^2/kT } elde edilebilir. Şekil 4 de iki farklı sıcaklıkta N2 için Maxwell-Boltzmann dağılımı çizilmiştir. Düşük sıcaklıklarda moleküler hızlar dar bir aralıkta dağılırken, yüksek sıcaklıklarda aralık genişlemektedir. Ayrıca eğrilerin maksimum değerleri sıcaklığa bağımlı olarak değişmektedir. Azot gazının aynı sıcaklıktaki bir boyuttaki hız dağılımı (Şekil 2) ile üç boyuttaki hız dağılımı (Şekil 4) karşılaştırınız. Şekil 4 dekine benzer, 3 farklı sıcaklık ve farklı molekül ağırlıkları için herhangi bir u değeri hesaplanma örneği, grafik verileri ve microsoft excel şablonuna için tıklayınız. Şekil 4 : 298 ve 1500 K de N2 moleküllerinin üç boyutta hız dağılımı. Daha önce kinetik teoriden hareketle moleküler hızların hız kareleri ortalamalı karekökü hızının \rm \sqrt{u^2}=\sqrt{3RT \over M } olduğunu göstermiştik. Moleküler hız dağılım eşitliğini kullanarak ortalama moleküler hızların nasıl değiştiğini hesaplayabiliriz. Bu amaçla; \rm \overline{u}^2 = \int_{u=0}^{u= \infty} u^2 {dN \over N} = 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} \int_{u=0}^{u= \infty} u^4 e^{- { 1 \over 2}mu^2/kT } du yazarsak eşitliğin integralinin sonucu \rm \overline{u}^2 = 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} \Big( {2kT \over m} \Big)^{5/2} { 3 \over 8 } \sqrt{ \pi } = {3kT \over m } verir. Sonuç olarak kinetik moleküler teori ile uygun olan \rm \sqrt { \overline{u}^2 } = \sqrt{ 3kT \over m} = \sqrt{ 3RT \over M} eşitlik elde edilmiş olur. Benzer şekilde ortalama hız \rm \overline{u}, değeri; \rm \overline{u} = \int_{u=0}^{u= \infty} u {dN \over N} yaklaşımı kullanılarak \rm \overline{u} = \sqrt{ 8kT \over \pi m} = \sqrt{ 8RT \over \pi M} şeklinde elde edilir. Bu hızlar dışında hız - olasılık grafiklerindeki maksimum olasılıklı hızı da belirleyebiliriz. Bu grafiğin maksimum değerine karşı gelir. Bunun için; \rm P_u = {dN/N \over du} = 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} u^2 e^{- { 1 \over 2}mu^2/kT } fonksiyonun du ye göre türevini sıfır yapan u değeri hesaplanmalıdır. \rm {dP_{u_{mp}} \over du_{mp}} = 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} \Big[ e^{- { 1 \over 2}mu_{mp}^2/kT } \cdot 2u_{mp} + u_{mp}^2 e^{- { 1 \over 2}mu_{mp}^2/kT } \cdot \Big( { -2 m u_{mp} \over 2kT } \Big) \Big] = 0 Burada \rm u_{mp} en olasılıklı hızı göstermektedir. \rm 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} \Big( e^{- { 1 \over 2}mu_{mp}^2/kT } \cdot 2u_{mp} \Big) = 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} \Big[ u_{mp}^2 e^{- { 1 \over 2}mu_{mp}^2/kT } \cdot \Big( { 2 m u_{mp} \over 2kT } \Big) \Big] eşitliğin her iki tarafı \rm 4 \pi \Big( {m \over 2 \pi k T} \Big)^{3/2} \Big( u_{mp}^2 e^{- { 1 \over 2}mu_{mp}^2/kT } \cdot 2u_{mp} \Big) bölünürse \rm 1- {2u_{mp}^2 \over 2kT} = 0 eşitliği elde edilir. Böylece maksimum olasılıklı hız için; \rm u_{mp}= \sqrt{ 2kT \over m} = \sqrt{ 2RT \over M} eşitliği elde edilir. Maxwell-Boltzmann Hız Dağılımı Örneği. Moleküler Hızlar Örneği.