İdeal gaz kanunları ve bu kanunlarından sapmalar hakkında fikir sahibi olduk. Hatta sapmaları açıklamak için deneysel bağıntılarda da söz ettik. Fakat neden gazların, ideal gaz kanunlarından saptıkları konusunda ayrıntılı teorik herhangi bir yaklaşımdan söz etmedik.
1873 yılında Hollandalı kimyacı J.D. van der Walls, gerçek gazların ideal gaz yasasından sapmalarını açıklamak için moleküler modele iki parametre ilave etti. PV=nRT ilişkisinden sapmanın nedeni, (1) gaz molekülleri tarafından işgal edilen hacmin, (2) moleküler arasındaki çekim kuvvetinin ihmal edilmesiydi.
n mol gaz V hacimli bir yere konulduğunda moleküllerin bu hacim içinde serbestçe hareket ederken hacimlerini ihmal etmiştik.Fakat moleküllerin hacimleri kabın hacmiyanıda ihmal edilemeyecek kadar fazla olabilir. Bu hacim dışarılanmış hacim (excluded volume) olarak adlandırılır. Bir mol gazın dışarılanmış hacmini b ile gösterirsek, PV= nRT eşitliğini
P(V - nb) = nRT
şeklinde düzenleyebiliriz. Dışarılanmış hacim, b,
sabit bir değere sahiptir ve herhangi bir gaz için karakteristik olup deneysel
verilerden hareketle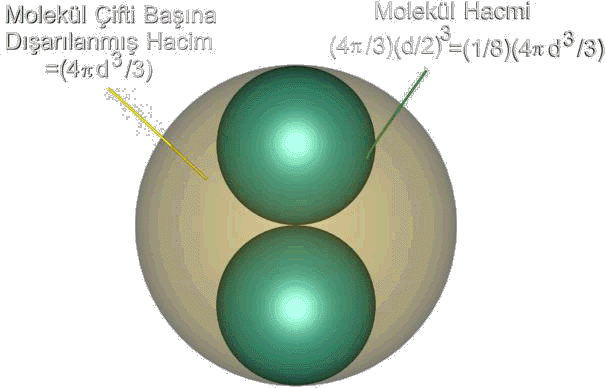 
elde edilebilir. b
nin molekül boyutuna bağımlılığını açıklamak için yandaki şekilden
yararlanabiliriz. Eğer gaz moleküllerinin d çaplı bir küre
olduklarını varsayarsak, iki molekülün merkezlerinin birbirlerine maksimum
yaklaştıkları durumda gölgeli olarak çizilmiş bir d yarıçaplı küre içerisinde
bulurlar. molekül çifti başına dışarılanmış hacim 4pd3/3
olacaktır. Mol başına düşecek dışarılanmış hacim ise
yukarıdaki eşitlikteki köşeli parantezler arasında kalan kısım molekül hacmi olup dışarılanmış hacim 4 kat daha fazladır.
İkinci van der Walls düzeltme terimi moleküller arasındaki çekim kuvvetleri ile ilgilidir. Düşük sıcaklıkta tüm gazların kinetik enerjilerinine karşın yoğunlaşma eğilimleri bu çekimin sonucudur. Bu sonucun tam olarak analizi zordur. Şekillerden de görüldüğü gibi gerçek gazlar çok düşük basınçlarda moleküller aralarında etkin çekim kuvvetleri oluşturamadıkları için dar basınç aralıklarında sıkıştırılabilmek föktörleri ideal gazların sahip olduğu z = 1 değerinden daha düşük değerler alabilmektedir. Bu beklenen basıncın ideal gazlardan beklenen değerin altında kalması demektir. İdeal bir gazdan beklenene P değerine ulaşabilmek için, bu P değerine P' değerinin ilave yapılması gerekir. İlave edilmesi gereken bu P' değeri, gazın özelliğine ve gazın kapladığı hacmin karesiyle ters orantılı olarak değişir. Bu gazın konsantrasyonu ile orantılı olması anlamını taşır. Böylece P' =n2/V2 olarak yazılır. Son olarak van der Walls denklemi
şekline ulaşır. Böylece PVT değerleri herbir gaz ve sıcaklık için kullanılabilecek hal eşitliği yazılmış olur. Bazı gazlar için a ve b değerleri aşağıdaki tabloda verilmiştir.
Tablo 1 : çeşitli gazlar için van der Walls sabitleri.
| Gaz | a / (L2 atm. mol-2) | b / (10-2 L mol-1) | Gaz | a / (L2 atm. mol-2) | b / (10-2 L mol-1) |
| Ar | 1.363 | 3.219 | H2O | 5.536 | 3.049 |
| C2H4 | 4.530 | 5.714 | H2S | 4.490 | 4.287 |
| C2H6 | 5.562 | 6.380 | He | 0.03457 | 2.370 |
| C6H6 | 18.24 | 11.54 | Kr | 2.349 | 3.978 |
| CH4 | 2.283 | 4.278 | N2 | 1.408 | 3.913 |
| Cl2 | 6.579 | 5.622 | Ne | 0.2135 | 1.709 |
| CO | 1.505 | 3.985 | NH3 | 4.225 | 3.707 |
| CO2 | 3.640 | 4.267 | O2 | 1.378 | 3.183 |
| H2 | 0.2476 | 2.661 | SO2 | 6.803 | 5.636 |
van der Walls Eşitliği ve Kritik
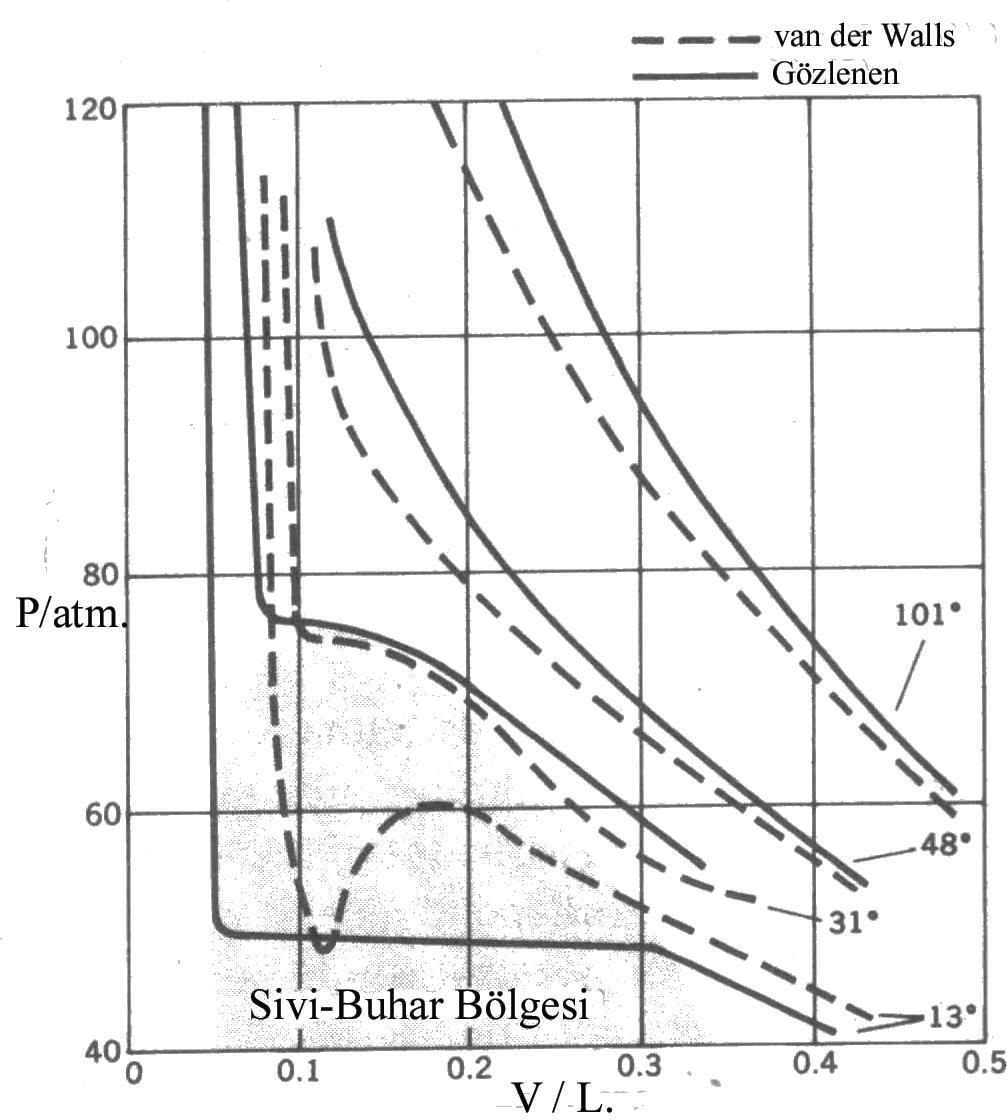
NoktaYandaki şekilde sıvı-buhar dengesi bölgesine yakın noktalardaki gaz davranışları van der Walls eşitliği kullanılarak karşılaştırılmıştır. Şekilden de görüldüğü gibi denel değerlerle eşitlikten elde edilen değerlerin uyumu açıkça görülmektedir. 1 mol gaz için basınç;
yazılabilir. dP/dV ve d2P/dV2 ye göre değişimi için;
ve
yazılabilir. Birinci ve ikinci türev kritik noktada 0 dır ve mol başına hacim, basınç ve sıcaklık Vc, Pc ve Tc dir. Bu noktada;
,
ve
yazılabilir. Bu üç eşitliklerden a , b ve R değerleri Pc, Vc, ve Tc değerlerine terimlerine bağlı olarak
şeklinde elde edilebilir. Kritik değerler kullanılarak a, b değeri
eşitliklerinden hesaplanabilir.
Deneysel veriler kullanılarak gazlar için karşılıklı haller ilkesine göre nasıl bir grafik ortaya çıkacağını daha önce göstermiştik (1). van der Walls eşitliğindeki a, b ve R değerleri kritik değerlere bağlı olarak yeniden yazılır ve Pr=P/Pc, Vr=V/Vc, Tr=T/Tc, değişimi gerçekleştirilirse
eşitliği elde edilebilir.
1 mol gaz için van der Walls eşitliğini
şeklinde yazabiliriz. ( 1- x )-1 in binomal açılımı;
( 1- x )-1 = 1 + x + x2 + . . .
şeklindedir. Yukarıdaki açılım ( 1- b/V )-1 ile karşılaştırılırsa x < 1 değerleri için uygun sonuçlar elde edilir. Serinin ilk üç teriminini dikkate alarak ifadeyi yeniden düzenlersek
yazılabilir. İkinci terime kadar olan kısım dikkate alınacak olursa van der Walls eşitliği ile tam uyum içerisinde olduğu görülür.
( b - a/RT ) terimi sıcaklığa bağlıdır ve tablodaki BV(T) değerlerine benzer. Yüksek sıcaklıklarda b terimi baskın hale gelir ve ( b - a/RT ), b nin sabit değerine yaklaşır. Düşük sıcaklıklarda ise; a/RT değeri, b teriminden daha baskın olur ve( b - a/RT ) düşük sıcaklıklarda negatif işaretli olur. Böylece Boyle sıcaklığının van der Walls sabitleri ile
veya
şeklinde ilişkili olduğunu kolayca görebiliriz.
Eğer a, b ve R nin değeri kritik değerlere bağlı olarak yerine konursa Boyle sıcaklığının
TBoyle=27Tc/8
ifadesi ile ilişkili olduğu görülür.
Gerçekte bu ilişki kabaca doğrudur tabloda Boyle sıcaklıkları görülmektedir.
Tablo 2 : çeşitli gazlar için Boyle sıcaklıkları, Kritik sıcaklıklar ve birbirine oranları.
| Gaz | TBoyle / K | Tc / K | TBoyle/Tc |
| H2 | 117 | 33.3 | 3.5 |
| He | 24 | 5.3 | 4.5 |
| CH4 | 497 | 190.2 | 2.6 |
| NH3 | 860 | 405.6 | 2.1 |
| N2 | 332 | 126.0 | 2.6 |
| O2 | 424 | 154.4 | 2.7 |
Gaz moleküllerinin bulundukları ortamda serbest hareketleri basıncın
düşüklüğü ve sıcaklığın yüksekliği ile birlikte artış gösterecektir. Gaz
taneciklerinin hareketleri ortamdaki gaz konsantrasyonuna, n/V, bağlı
olarak diğer gaz molekülleri tarafından büyük ölçüde engellenir. Bu durumda kabın
çeperine ulaşabilecek taneciklerin E enerjisininde artması gerekir. Kinetik enerjileri
ancak belli E değeri üzerinde olan tanecikler kabın çeperine ulaşabilecektir.
Enerjileri E nin üzerinde bulunan taneceiklerin gaz taneciklerinin sayısı exp(-E/RT) ile orantılıdır. Öte yandan, E
enerjisinin büyüklüğü 1 mol gaz için molar hacim 
ile ters orantılı olacaktır ( E =
A/) . Böylece yukarıdaki
eşitlik exp(-A/RT) şeklinde yeniden düzenlenebilir.
Bu durumda ölçülen basınç P ise, Pi
ideal basınç olmak üzere;
eşitliği ile verilebilir. van der Walls denkleminde olduğu gibi i= - b değişimi gerçekleştirilirse Dieterici hal denklemi
şeklinde yazılabilir. n mol gaz için bu hal denklemi
şeklinde yazılabilir. van der Walls denkleminde olduğu gibi kritik sabitler belirlenebilir. 1 mol gaz için yukarıdaki türevleri işlemlerini uygulamadan önce Dieterici hal denkleminin logaritması alınırsa;
yazılır ve sonra lnP nin hacime göre birinci ve ikinci türevleri 0 yapan durum araştırılırsa;
eşitlikleri elde edilebilir. Bu eşitliklerden kritik büyüklükler
Vc=2b , Tc=A/4Rb
şeklinde elde edilir. Bu değerler Hal denkleminde yerine konursa Pc için
Pc=Ae-2/4b2
değeri elde edilir. van der Walls ve Dieterici hal denklemleri arasında kritik değerler açısından kaynaklanan bu farkın nedeni yaklaşımdan kaynaklanmaktadır. Gerekli yaklaşımlar yapılırsa Dieterici denkleminden van der Walls denklemine ulaşılabilir. ex üstel fonksiyonu seriye açılırsa;
ifadesi elde edilir. Dieterici hal denkleminde yer alan exp(-A/RT) büyüklüğü seriye
açılır ve ikinci terimden sonraki terimler ihmal edilecek olursa
bağıntısı elde edilir. Son ifade Dieterici denkleminde yerine konur ve A basınç düzeltme faktörü van der Walls denklemindeki a basınç düzeltme faktörüne eşit alınırsa van der Walls denklemi elde edilir.
