Basmaklı (Reaktif Son Grup)(Kondensasyon) Polimerizasyonu
1929 da W. H. Carothers polimerleri; kondensasyon polimerleri ve katılma polimerleri olmak üzere iki grup altında topladı. Kondensasyon polimerlerindeki tekrarlanan birimlerinin formülünde monomerlerindeki bazı atomlar yoktur. Örneğin; polyester bifonksiyonel monomerlerin kondensasyon reaksiyonları sonucu su eliminasyonu ile gerçekleşir.
\rm x \; HO-R-OH \; + \; x \; HO-CO-R'-CO-OH \; \rightarrow \; H-[O-R-O-CO-R'-CO-]_x-OH \; + \; (2x-1)\; H_2O
Katılma polimerlerinde küçük molekül kaybı meydana gelmez. Katılma polimerlerinin en önemli grubu doymamış vinil monomeri türevidir.Katılma polimerlerinde küçük molekül kaybı meydana gelmez. Katılma polimerlerinin en önemli grubu doymamış vinil monomeri türevidir.
\rm m \; H_2C=CHX \; \rightarrow \; -[-CH_2-CHX-]_m-
Carother'in orjinal fikri Flory tarafından polimerin bu iki tipindeki mekanizma üzerinde durularak düzeltildi. Kondensasyon polimerleri genellikle reaktif grupların adım adım reaksiyonu ile oluşur. Tablo 1 de zincir ve basamaklı polimerizasyonun farkları gösterilmiştir. Tablo 1 de basamaklı polimerizasyon ile katılma polimerizasyonu arasındaki farklar gösterilmiştir.
Tablo 1 :
Zincir ve Basamaklı Polimerizasyon mekanizmasının ayırt edici özellikleri.
| Zincir Polimerizasyonu |
Basamaklı Polimerizasyon |
i. Reaksiyonun ilerlemesi zincire tekrarlanan birimin katılması ile meydana gelir. |
i. İki fonksiyonel türün varlığında reaksiyon gerçekleşir. |
ii. Monomer konsantrasyonu reaksiyon boyunca gittikçe azalır. |
ii. Monomer polimerizasyon derecesi (DP) 10 olduğunda, ortadan kalkar. % 1 den daha az monomer kalır. |
iii. Yüksek molekül ağırlıklı polimer oluşur. Polimerin molekül ağırlığı reaksiyon boyunca küçük değişimlere uğrar. |
iii. Polimerin molekül ağırlığı reaksiyon boyunca artar. |
iv. Reaksiyon zamanının artması ile yüksek verim meydana gelir fakat molekül ağırlığı çok değişmez. |
iv. Reaksiyon zamanının arttırlması ile esasen daha yüksek molekül ağırlıklı polimer elde edilir. |
v. Reaksiyon karışımı, yalnızca monomer, yüksek molekül ağırlıklı polimer ve çok az miktarda büyüyen zincir içerir. |
v. Herhangi bir adımda tüm moleküler türler dağılımı hesaplanabilir. |
Basmaklı Polimerizasyonun Mekanizması
Lineer polimerleri verirler. Polifonksiyonel monomerler molekül başına ikden daha fazla fonksiyonel grup içerirler ve dallanmış veya çapraz bağlı üç boyutlu polimerleri verirler. Lineer ve çapraz bağlı polimerlerin özellikleri birirlerinden çok farklıdır.
Tablo 2 de bazı basamaklı polimerizasyon reaksiyonları gösterilmiştir.
Basmaklı Polimerizasyon Kinetiği
Bir grubun reaksiyon hızının, grubun takılı olduğu molekülün boyutundan bağımsız olduğunu söyleyebiliriz. Bu düşünce deneysel verilerle uyuşur. Bir homolog serideki kondensasyon reaksiyonlarının hız sabitleri, zincir uzunluğundan bağımsız asimtotik bir değere ulaşır ve molekül ağırlığındaki artmayla düşüş eğilimi göstermez. Elbette büyük molekülerin seyrelme etkisi, reaktif grupların sabit molar bileşimleri için ayarlanarak hesaplanmalıdır. Ayrıca; monofonksiyonel ve bifonksiyonel reaktiflerin hız sabitleri, bifonksiyonel bileşiğin reaktif gruplarının yeterince uzun zincirlerle birbirinden ayrılmasıyla aynı değere ulaşır.
Tablo 3 :
Homolog Serilerde \rm H(CH_2)_nCOOH ve \rm (CH_2)_n(COOH)_2 formülleri ile gösterilen bir ve
iki karboksilli asitlerin etil alkol ile HCl katalizörlüğünde esterleşme hız sabitleri \rm (Eşdeğer gram / Litre)^{-1} \; ^{s-1}.
| n değeri |
\rm k_A \times 10^4 \; (25 \; ^oC)
( monobazik asidin esterleşmesi ) |
\rm k_B \times 10^4 \; (25 \; ^oC)
( dibazik asidin esterleşmesi ) |
| 1 |
22.11 |
|
| 2 |
15.3 |
6.0 |
| 3 |
7.5 |
8.7 |
| 4 |
7.4 |
8.4 |
| 5 |
7.4 |
7.8 |
| 6 |
|
7.3 |
| 8 |
7.5 |
|
| 9 |
7.4 |
|
| 11 |
7.6 |
|
| 13 |
7.5 |
|
| 15 |
7.7 |
|
| 17 |
7.7 |
|
Glikol ve bir dibasik asidin polyesteri oluşturmak üzere tepkimesi basmaklı polimerizasyon kinetiği için iyi bir örnektir. Bu tip bir reaksiyon asit ile katalizlenir. Eğer güçlü bir asit katılmazsa asdin ikinci bir molekülü katalizleme olaynı üstlenir. Reaksiyon karboksil gruplarının konsantrasyonlarındak değişim kontrol edilerek izlenebilir.
\rm - { d[COOH] \over dt } = k[COOH]^2[OH]
Eğer eğer karboksil ve hidroksil gruplarının konsantrasyonu C kadarsa eşitlik
\rm - { dC \over dt } = kC^3
ve
\rm 2kt = {1 \over C^2 } - Sabit
şeklinde düzenlenebilir.
p parametresi ile t zamanında reaksiyona girmiş olan fonksiyonlu grupların kesrini gösterecek olursak herhangi bir t anında
reaksiyon vermemiş fonksiyonlu grupların kesri 1 - p ye eşittir. Böylece;
\rm C=C_o(1-p)
ve
\rm 2C_o^2 k t = {1 \over (1-p)^2 } - Sabit
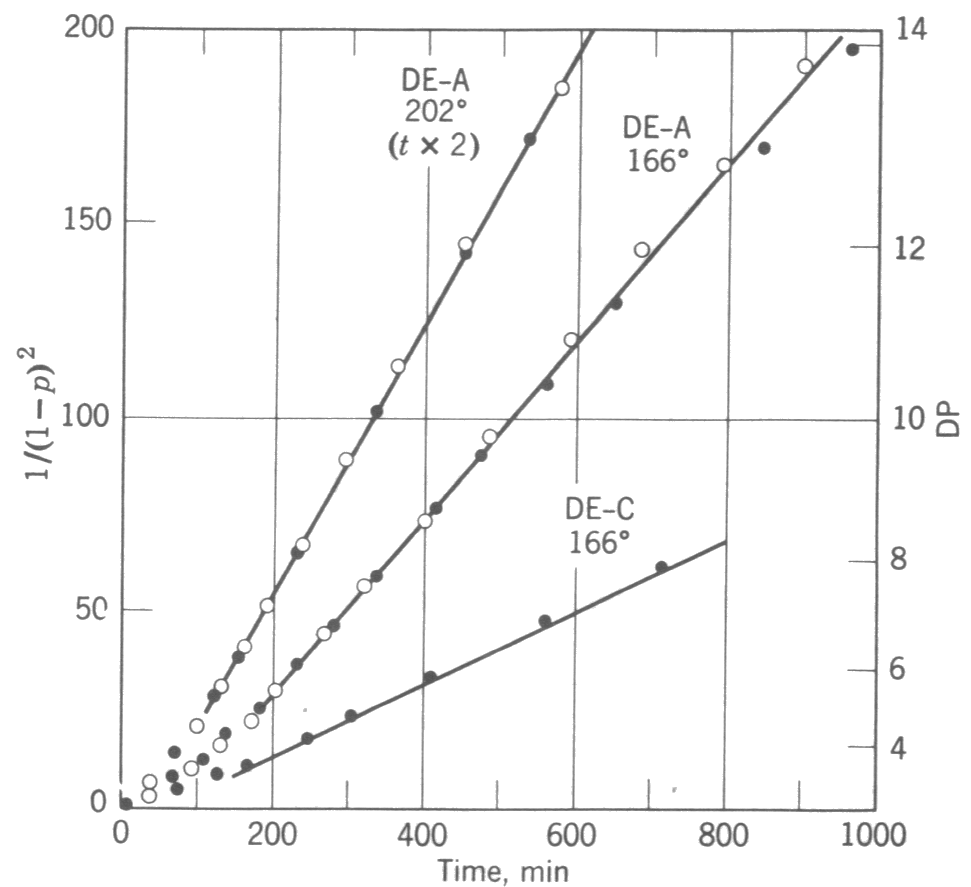
Şekil 1 :Dietilen glikolün (DE)adipik asit (A)ve kaproik asit (C) ile reaksiyonu. 202 \rm ^oC deki zamanlar 2 ile çarpılmıştır.
|
Elde edilebilir. Eşitlikten zamana karşı \rm 1/(1-p)^2 değişiminin lineer olması gerektiği söylenebilir.
Dietilen glikol ile adipik asit ve dietilen glikol kaproik asit arasında gerçekleşen polimerizasyon tepkimeleri için
zaman - \rm 1/(1-p)^2 ilişkisi Şekil 1 de gösterilmiştir.
Geniş reaksiyon aralıkları dikkate alınırsa eşitlikte sapmalaar gözükür.
Lineer kısım genelllikle %83-93 gibi dar bir dönüşüm aralığında gözlenir.
Düşük dönüşümlerdeki sapma, monomerin polimere dönüşmesi sonucu reaksiyon ortamın polaritesinin değişmesinden,
ve yüksek dönüşümlere ulaşıldığında ters reaksiyon hızının artmasına bağlanabilir.
Yalnızca bifonsiyonal reaktanlar bulunduğunda hiçbir yan reaksiyon meydana gelmez.
Bu durumda reaksiyona girmemiş karboksil gruplarının sayısı, sistemdeki moleküldeki toplam molekül sayısına , N, eşittir.
Asit yada hidroksil grupları ayrı ayrı yapısal birimler olarak düşünülürlerse; karboksil gruplarının başlangıçtaki sayısı,
yapısal birimlerde bulunan \rm N_o a eşit olacaktır. Polimerizasyon derecesi sayı-ortalaması \rm \overline{\chi} _n ;
\rm \overline{\chi} _n = \overline{DP} _n = { N_o \over N } = { C_o \over C } = { 1 \over 1 - p }
eşitliği ile verilir. Şekil 1 in sağında görüldüğü gibi ortalama polimerizasyon derecesi, \rm \overline{DP} _n, katalizlenmemiş esterleşme reaksiyonlarında yüksek polimerizasyon değerlerine ulaşmak için polimerizasyon sürelerinin oldukça uzun tutulması gerektiğini göstermektedir. Bunun nedeni moleküllerin reaktifliğinin az olmasından değil reaksiyonun üçüncü mertebeden olmasına bağlıdır. Sisteme az miktarda katalizör olarak asit katılır ve reaksiyon süresinde konsantrasyonu sabit tutulursa, kinetik eşitlik ikinci dereceden bir eşitlik olarak

Şekil 2 :% 0.4 mol p-toluensülfanik asit ile katalizlenmiş 109 \rm ^oC de Dietilen glikol ile adipik asidin polyesterleşmesi.
|
\rm - { d[COOH] \over dt } = k'[COOH][OH]
\rm - { dC \over dt } = k'C^2
\rm C_ok't = { 1 \over 1-p } + Sabit
\rm C_ok't = \overline{DP} _n + Sabit
veya
\rm \overline{DP} _n = C_ok't + Sbt
şeklinde düzenlenebilir. Şekil 2 de asit katalizli mekanizmaya ait deneysel bir çalışma görülmektedir.
Soru 1 :
Aşağıdaki 25 yuvarlak asit molekülerini gösterirse zamanla p ve değerlerini ne olacağını aşağıdaki çizimlere göre hesaplayınız.


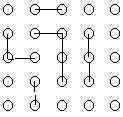

\rm \qquad t=0 \qquad
\rm \; \; \; \; \; \; \; \; t=t_1 \qquad
\rm \qquad t=t_2 \qquad
\rm \qquad t=t_3 \qquad
|
Yanıt 1 :
p zamanla reaksiyona girmiş moleküllerin kesrini \rm (N_o-N)/N_o ve ; \rm 1/(1-p) veya \rm N_o/N olduğundan
t = 0 anı için;
\rm p = {N_o - N \over N_o } = 0 \qquad \overline{DP}_n = { 1 \over 1 - p }
\rm p = {25-25 \over 25 } = 0 \qquad \overline{DP}_n = { 1 \over 1 - 0 } = 1
t = \rm t_1 anı için;
\rm p = {N_o- N \over N_o } = 0 \qquad \overline{DP}_n = { 1 \over 1 - p }
\rm p = {25-22 \over 25 } = {3 \over 25 } \qquad \overline{DP}_n = { 1 \over 1 - { 3 \over 25 } } = {25 \over 22 }
t = \rm t_2 anı için;
\rm p = {N_o- N \over N_o } = 0 \qquad \overline{DP}_n = { 1 \over 1 - p }
\rm p = {25-16 \over 25 } = {9 \over 25 } \qquad \overline{DP}_n = { 1 \over 1 - { 9 \over 25 } } = {25 \over 16 }
t = \rm t_3 anı için;
\rm p = {N_o- N \over N_o } = 0 \qquad \overline{DP}_n = { 1 \over 1 - p }
\rm p = {25-8 \over 25 } = {17 \over 25 } \qquad \overline{DP}_n = { 1 \over 1 - { 17 \over 25 } } = {25 \over 8 }
Soru 2 :
Eşit mol sayılarında etilen glikol ve teraftalik asit kullanılarak üretilen polietilenteraftalattan 4.64 g. alınarak,
örnek 0.1 M NaOH ile titre edildiğinde 20 \rm cm^3 NaOH çözeltisi harcanmıştır.
Bu aşamada elde edilen PET in \rm \overline{DP}_n değeri nedir?
Kullanılan NaOH in mol sayısı;
\rm n_{NaOH} = \big( 0.1 \; M \; NaOH \big) \times \big( 20 \times 10^{-3} \; L \big) = 2 \times 10^{-3} \; mol NaOH
1.0 mol NaOH ile tepkime verecek PET miktarı ise; PET in sayı ortalaması molekül ağırlığını verecektir.
\rm \overline{M}_n = \big( 1.0 \; mol \; NaOH \big) \Big( { 4.64 \; g. PET \over 2 \times 10^{-3} \; mol NaOH } \Big) = 2320 \; g. \; mol^{-1}
 yapısında tekrarlanan birimin mol tartısı 192 akb olduğundan; polimerizasyon derecesi; yapısında tekrarlanan birimin mol tartısı 192 akb olduğundan; polimerizasyon derecesi;
\rm \overline{DP}_n = { \overline{M}_n \over \overline{M}_o }
\rm \overline{DP}_n = { 2320 \; g. \; mol^{-1} \over 192 \; g. \; mol^{-1} } \simeq 12
olarak hesaplanır.
Lineer Kondensasyon Polimerlerinde Molekül Ağırlığının Denetlenmesi :
Polimerik maddelerin özellikleri molekül ağırlığı ile önemli ölçüde değiştiğinden, polimerik maddenin molekül ağırlığını kontrol altında tutmak önemlidir. Uygulamalarda yüksek molekül ağırlıkları gerekli olabileceği gibi düşük molekül ağırlıklı polimerlere de gerek duyulabilir. Basamaklı polimerizasyon reaksiyonlarında polimerizasyonun derecesi reaksiyon süresinin bir fonksiyonu olduğundan istenen molekül ağrılığı civarına ulaşıldığında reaksiyon durdurulabilir. Bunun için örneğin reaksiyon karışımı soğutulabilir. Bununla beraber daha sonra ısının artışı reaksiyonun yeniden ilerlemesine neden olur. Bu nedenle daha iyi bir çözüm reaksiyon karışımının bileşimini değiştirerek gerçekleştirilebilir. Bu amaçla ya monomerlerden birinin konsantrasyonu değiştirilir ya da reaksiyon ortamına tek fonksiyonlu bir madde katılabilir. Bu tür bir karışımda reaksiyona giren maddelerden birinin tümünün tüketilmesi ve bütün zincirlerin her iki yönde aynı fonksiyonlu gruplarla sonlanmasıyla durdurulmuş olur.
A-A ve B-B iki fonksiyonlu monomerlerle gerçekleşecek basamaklı polimerizasyon reaksiyonunda;
Başlangıçta alınan A gruplarının sayısı \rm N_A,
ve Başlangıçta alınan B gruplarının sayısı \rm N_B olsun.
Reaktiflik oranı için \rm r = { N_A \over N_B } yazılabilir.
Eğer bu oran 1 ise büyük molekül ağırlıklı polimerler elde edilir.
Eğer \rm N_A < N_B r \rm < 1 olacaktır.
p yi reaksiyonun ilerleme parametresi (reaksiyona giren A gruplarının kesri) olarak düşünürsek,
ortamdaki toplam birim sayısı \rm (N_A+N_B) \over 2 olacağından;
ortamdaki toplam birim sayısı
\rm { N_A + { N_A \over r } \over 2 } = { N_A \over 2 } \Big( {1+ { 1 \over r}} \Big)
ifadesi elde edilebilir. Herhangi bir andaki zincir sonlarının sayısı ise;
\rm N_A (1-p) A ile sonlanmış zincir sonlarının sayısı ve B ile sonlanmış zincir sayısı \rm N_B -N_Ap olacağından
\rm N_B - N_Ap = N_A \Big( { 1 \over r } - p \Big)
olacaktır. Bu durumda zincir sonlarının toplam sayısı;
\rm N_T = N_A(1-p)+ N_A \Big( { 1 \over r } - p \Big) = N_A \Big( 1 - 2p + { 1 \over r } \Big)
olacaktır. Bu durumda polimerizasyon derecesi \rm \overline{DP}_n;
\rm \overline{DP}_n = { \text{ Toplam Birim Sayısı } \over \text{ Zincir Sonlarının Toplamı } }
= { N_A \Big( {1 + { 1 \over r } } \Big) \over 2 N_A \Big( {1 - 2p + { 1 \over r } } \Big) } =
{ { 1+ {1 \over r }} \over 2 \Big( {1 + { 1 \over r } -2p } \Big) }
\rm
\overline{DP}_n =
{
{ r \; + \; 1 \over r }
\over
{
r + 1 - 2rp
\over
r
}
}
\rm \overline{DP}_n = { 1 + r \over 1+r -2rp }
p = 1 için;
\rm \overline{DP}_n = { 1 + r \over 1 - r }
olacaktır.
Örneğin r = 0.99 için; \rm \overline{DP}_n = 199 çıkar ki bu 199 birimin birleştiğini gösterir.
Polimerizasyon oratamına %1 mol B den ilave edilecek olursa \rm { N_A \over N_B } = { 100 \over 101 } olacaktır.
Bu durumda \rm \overline{DP}_n = 201 olarak olacaktır. Mol tartısı bu hesaba denetlenebilir.
Fonksiyonlu grupların sayısı 2 den fazlaysa, f; monomerdeki fonksiyonlu grup sayısı, \rm N_o;
başlangıçtaki monomer sayısı, N = reaksiyon sonundaki molekülerin sayısı,
p; bağ yapmak üzere kullanılan fonksiyonlu grupların başlangıçtaki fonksiyonlu grupların sayısına oranı olmak üzere;
reaksiyon sırasında moleküllerin sayısı \rm N_o dan N düşeceğinden \rm (N_o-N) tane bağ oluşacaktır.
Bir tek bağın oluşması için iki fonksiyonlu grubun reaksiyon vermesi gerektiğinden;
\rm p = { 2(N_o-N) \over N_o f }= { 2 \over f } - { 2N \over N_o f }
bağıntısı elde edilir. Polimerizasyon derecesi sayı-ortalaması \rm \overline{DP}_n = N_o/N olduğundan;
\rm p= { 2 \over f } - { 2 \over \overline{DP}_n f }
\rm p= { 1 \over 1- { fp\over 2 } }
bağıntısı elde edilir. İki fonksiyonlu monomerler için f = 2 olacağından;
\rm \overline{DP}_n = { 1 \over 1 - p }
bağıntısına dönüşür. Fonksiyonlu grup sayıları farklı monomerlerin karışımları için de kullanılabilir.Böyle bir polimerizasyon reaksiyonu için ortalama (sayı-ortalaması) kullanılmalıdır. Örneğin 2 mol gliserin ile 3 mol adipik asit arasındaki bir polikondensasyon reaksiyonu için, 2x3 + 3x2 = 12 fonksiyonlu grup bulunmaktadır. Molekül başına ortalama fonksiyonlu grup sayısı 12/5 = 2.4 olarak elde edilir. Reaksiyon %75 ilerlediğinde ( p = 0.75 ) ise; polimerizasyon derecesi sayı ortalaması 10 olarak hesaplanır.
Üç Boyutlu Kondensasyon Polimerizasyonu
Kondensasyon reaksiyonundaki monomerin birinde bile ikiden daha fazla fonksiyonlu grup varsa, reaksiyon sonucu üç boyutlu bir polimerik yapı ele geçer. Eğer zincirlerden biri diğer bir zinicir ile kondensasyon reaksiyonu verirse, çapraz bağ oluşumu meydana gelir. Reaksiyon karışımında sonsuz büyük bir polimer şebekesinin meydana gelmesi, bir başka deyimle bir jel oluşumu ile sonuçlanır. Jelin Meydana gelmesi ile birlikte iki farklı kısım meydana gelir.
Polimerizasyon jel noktasının ötesine geçerse jel büyür ve vizkoz sıvı olan karışım vizkozitesi sonsuz olan esnek bir madde haline gelir. Jel noktasında karışımın molekül ağırlığı sayı-ortalaması düşük olduğu halde, molekül ağırlığı ağırlık ortalaması sonsuz (büyük) olur.
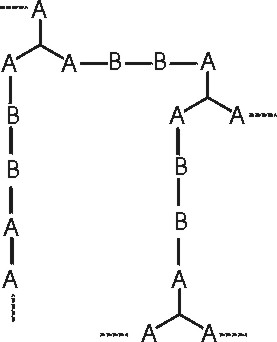
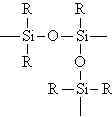
Şekil 3 : 2 ve 3 fonksiyonlu monomerlerin birlikte polimerleşmesi.
|
Jel Noktasının Belirlenmesi
Polikondensasyon reaksiyonlarında jel noktasının belirlenmesi için öncelikle \rm \alpha ile gösterilen dallanma katsayısının tanımlanması gerekir.
Bu katsayı; dallanmış bir birimdeki bir fonksiyonlu grubun yine dallanmış bir başka fonksiyonlu grupla
reaksiyon verme şansını gösterir. A-A-A, A-A, ve B-B monomerleri söz konusu ise;
reaksiyonlar sonucuŞekil 3 deki yapıya benzer bir yapı meydana gelebilir.
Eğer \rm \alpha < 1/2 ise; herbir zincirin bir dallanma birimi ile reaksiyon verme şansı birden az,
reaksiyon vermemiş iki fonksiyonlu bir grupla sonlanmış olma sansı birden fazladır.
Eğer \rm \alpha < 1/2 ise; şebeke sonsuz büyümez ve molekül yapısının büyüklüğü sınırlı kalır.
\rm \alpha > 1/2 durumunda ise; dallanmış grupla reaksiyon verme şansı birden büyüktür.
\rm \alpha = 1/2 durumu çapraz bağlı yapıyı elde etmek için kritik bir değerdir.
Bu kritik değer f fonksiyonlu grupların kesri olmak üzere
\rm \alpha _c = { 1 \over f -1 }
ifadesi ile hesaplanabileceği bulunmuştur. Deneysel ölçümler yapılmaksızın \rm \alpha değeri hesaplanmak istenirse p reaksiyon ilerleme parametresi kullanılarak hesaplamalar yapılmalıdır.
-
Reaksiyon karışımında yalnızca üç fonksiyonlu monomerler varsa; bu sistemde bir dallanma birimi üzerindeki fonksiyonlu gruplardan birinin bir başka dallanma birimine bağlanma olasılığı, fonksiyonlu grubun reaksiyon verme olasılığına eşittir ( \rm \alpha = p).

-
Reaksiyon ortamındaki monomerlerden bir 3 fonksiyonlu ve diğeri 2 fonksiyonlu ise ve reaksiyon ortamındaki A gruplarının sayısı B gruplarının sayısına eşit ise; A grubunun B ile reaksiyon vermesi (olasılık p) ve daha sonra B-B biriminin diğer ucundaki B fonksiyonel grubunun başka bir A grubu ile tepkime vermesi gereklidir (olasılık p). Bu nedenle dallanma katsayısı bu iki olasılığın çarpımına eşit olacaktır ( \rm \alpha = p^2 ).

-
Reaksiyon karışımında iki farklı 2 fonksiyonlu monomer ve 3 fonksiyonlu bir monomer söz konusu da olabilir
(A-A, A-A-A, B-B). A ve B fonksiyonlu grupları için reaksiyon ilerleme parametresi \rm p_A ve \rm p_B ,
\rm \rho ; dallanmış birimler üzerindeki A gruplarının sayısının toplam A grubunları sayısına oranı olmak üzere
\rm \alpha =f(r,r,p) şeklindedir. \rm \alpha için;
\rm \alpha = { p_Ap_B \rho \over 1 - p_Ap_B(1- \rho) }
yazılır. Ayrıca \rm r = N_A / N_B ve \rm p_B=rp_A eşitlikleri kullanılarak son eşitlik;
\rm \alpha = { p_A^2 \rho \over 1 - p_A^2(1- \rho) }
olarak elde edilir.
Jel noktasına erişildiğinde karışımın akışkanlığı birdenbire biter.
Bu karışımda gaz kabarcıklarının kesilmesi ile anlaşılır.
Bir yöntemle reaksiyon vermemiş grupların sayısı belirlenerek p elde edilebilir.
Gliserin ile iki karboksilli asitler arasındaki tepkimeler için p = 0.765 için jel oluşumu gözlenmiştir.
Bu sistem için \rm \alpha _c = p = 0.58 olarak elde edilir.
Değerin 0.5 den farklı olmasının nedeni gliserindeki OH gruplarının birinin reaktifliğinin
diğerlerinden farklı olmasından kaynaklanır.
|








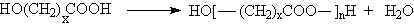

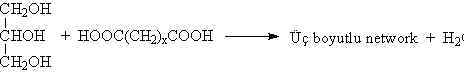
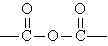
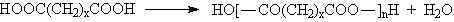
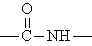
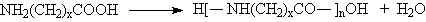

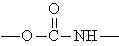



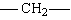
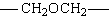
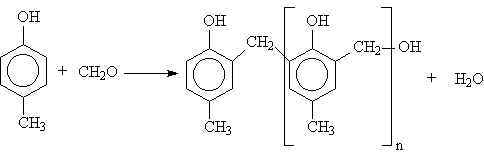
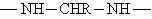
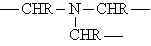
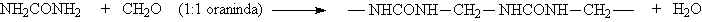
 fazlalığında üç boyutlu network yapısı oluşur.
fazlalığında üç boyutlu network yapısı oluşur.
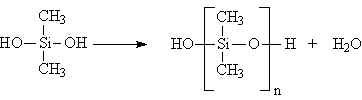



 yapısında tekrarlanan birimin mol tartısı 192 akb olduğundan; polimerizasyon derecesi;
yapısında tekrarlanan birimin mol tartısı 192 akb olduğundan; polimerizasyon derecesi;