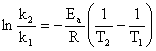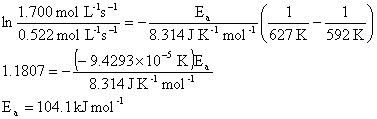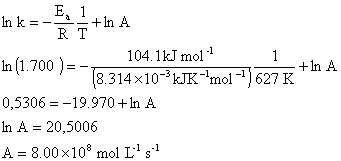LOGARİTMA :
a ve y gerçek sayılar olmak üzere;
ax = y
eşitliğini sağlayan x sayısına y sayısının a tabanına göre logaritması denir ve
x = logay
şeklinde gösterilir.
LOGARİTMANIN
GENEL ÖZELLİKLERİ :
Üstel
Sayıların Logaritması :
m sayısının n nci merteden üssünün
logaritması m sayısının logaritmasının n
ile çarpımına eşit olup
şeklinde gösterilir. Bu eşitliğin doğruluğunu
aşağıdaki gibi gösterebiliriz.
ifadesinin her iki tarafının a tabanına göre logaritması;
olacağından
ve ayrıca;
yazılır ve logaritması alınırsa;
elde edilir. Yukarıdaki x değeri yerine konulursa;
elde edilir.
Çarpımın
Logaritması :
m ve n sayılarının çarpımının logaritması bu sayılarının logaritmaları
toplamına eşittir.
Bunun doğruluğunu aşağıdaki gibi gösterebiliriz.
her iki eşitliğinin de a tabanına göre logaritması alınırsa
yazılır. Ayrıca
eşitliğin her iki tarafının a ya göre logaritması alınırsa
x ve y
değerleri yerine konulursa;
elde edilir.
Bölümün Logaritması :
m ve n sayılarının çarpımının logaritması bu sayılarının logaritmaları
faarkına eşittir.
Bunun doğruluğunu aşağıdaki gibi gösterebiliriz.
her iki eşitliğinin de a tabanına göre logaritması alınırsa
yazılır. Ayrıca
eşitliğin her iki tarafının a ya göre logaritması alınırsa
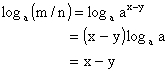
x ve y
değerleri yerine konulursa;
elde edilir.
Değişik Tabanlı Logaritma :
Bir m sayısının b tabanına göre
logaritması bilinirse a tabanına
göre logaritmasının nasıl
hesaplanacağını görelim.
ise; 
yazılabilir. Bu
eşitliğin her iki tarafının b tabanına
göre logaritması alınırsa
ve
bağıntısı elde edilebilir. x değeri yukarıdaki
eşitlikte yerine konursa
bağıntısı elde edilebilir (Örnek 1,
2, 3 ).
Örnek : 
sayısının değerini
logaritma kurallarından yararlanarak hesaplayınız.
Çözüm :
Örnek : Bir çözeltinin
asitliği pH ölçüsü ile ortamdaki hidrojen iyonlarının konsantrasyonuna
bağlı olarak 
şeklinde ifade
edilir. Saf suyun 25.0 oC deki pH değeri ise 7.0 dir. HCl %100
iyonlaştığını düşünerek, 100 mL suya 0.1, 0.2, 1.0, 2.0, 10.0 ve 20.0 mL 0.1 M
lık HCl çözeltisinden ilave edilmesi çözeltideki H+
konsantrasyonunun ve pH nasıl değiştiğini hesaplayarak çözelti hacmine karşı
grafiklerini çiziniz.
Çözüm :
Asidin başlangıç konsantrasyonu
ve hacmi 
ise, 
kadar asit ilave
edildiğinde yeni konsantrasyonu 
;
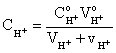
eşitliğinden hesaplanabilir.
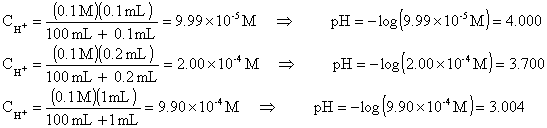
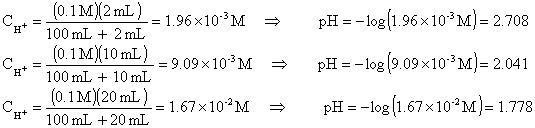
- Vtoplam grafiği, pH-Vtoplam
grafiği
Örnek : Kimyasal reaksiyonların pek çoğu için reaksiyon
hızının sıcaklığa bağımlılığı 
eşitliği ile
verilebilir. 
reaksiyonu için 319
ve 354 oC deki hız sabiti 0.522 ve 1.700 mol L-1 s-1
dir. Buna göre Ea ve A değerinin ne olduğunu hesaplayınız.
Çözüm :
