FONKSİYONLAR :
Açısal Fonksiyonlar
 Fonksiyon
basitçe bir veya birçok değişken büyüklüklere bağlı olarak değişen büyüklük
olarak tanımlanabilir. Fonksiyon içindeki değişenlerin (bağlı değişen)
büyüklükleri bize fonksiyonu değerinin ne olacağını gösterir. Örneğin bundan önceki
kısımda belli miktardaki bir gazın sabit sıcaklıkta basıncı hacmin artmasıyla
arttığı görülmüştür. Böyle bir durum P(V) şeklinde ifade edilebilir. Eğer
sıcaklık artarsa basıncın yine arttığı görülür. Bu durmda basınç P; P(V,T)
şeklinde değişeceği söylenebilir. Ve eğer kap içerisindeki gaz miktarı
arttırılırsa basıncın arttığı görülür ki; P(n,V,T) olduğu söylenebilir. Fakat
burada basnıncın n, V, T değişkenlerinin değerlerine bağlı olarak değer alacağı
söylenebilir fakat aralarındaki
matematiksel ilişkinin nasıl olduğuna dair herhangi bir şey söylenemez.
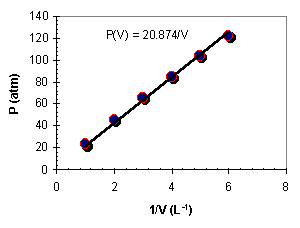
Kaartezyen koordinatlar anlatılırken kullanılan V değerleri kullanılarak 1/V
değerlerine karşı P değerleri grafik edilirse yandaki grafik elde edilir.
Burada basıncın hacmin bir fonksiyonu olarak nasıl değiştiği P(V)=20.78/V
eşitliği ile daha ayrıntılı olarak gösterilmiştir. Biraz önce basıncın yalnızca
hacmin değil aynı zamanda sıcaklığın ve mol sayısının da fonksiyonu olduğunu
ifade etmiştik. Oysa bu eşitlikte bu sıcaklık ve mol sayısı görülmemektedir.
Bunun nedeni mol sayısı ve sıcaklığın sabir tutulması nedeniyle bu iki
parametrenin 20.78 sabit değeri içinde bulunduğu düşünülebilir. Fakat denel bir
çalışma yapmaksınız sıcaklık ve mol sayısının bu sabit değer içine nasıl
dağıldığını söyleyemeyiz. Benzer
şekilde hacim ve mol sayısı sabit tutularak basınç üzerine sıcaklığın etkisi
P(T) veya sıcaklık ve hacim sabit tutularak basınç üzerine mol sayısının etkisi
incelenebilir P(n). Eğer bu tüm ilişkiler birleştirilirse ideal bir gaz için
Fonksiyon
basitçe bir veya birçok değişken büyüklüklere bağlı olarak değişen büyüklük
olarak tanımlanabilir. Fonksiyon içindeki değişenlerin (bağlı değişen)
büyüklükleri bize fonksiyonu değerinin ne olacağını gösterir. Örneğin bundan önceki
kısımda belli miktardaki bir gazın sabit sıcaklıkta basıncı hacmin artmasıyla
arttığı görülmüştür. Böyle bir durum P(V) şeklinde ifade edilebilir. Eğer
sıcaklık artarsa basıncın yine arttığı görülür. Bu durmda basınç P; P(V,T)
şeklinde değişeceği söylenebilir. Ve eğer kap içerisindeki gaz miktarı
arttırılırsa basıncın arttığı görülür ki; P(n,V,T) olduğu söylenebilir. Fakat
burada basnıncın n, V, T değişkenlerinin değerlerine bağlı olarak değer alacağı
söylenebilir fakat aralarındaki
matematiksel ilişkinin nasıl olduğuna dair herhangi bir şey söylenemez.
Kaartezyen koordinatlar anlatılırken kullanılan V değerleri kullanılarak 1/V
değerlerine karşı P değerleri grafik edilirse yandaki grafik elde edilir.
Burada basıncın hacmin bir fonksiyonu olarak nasıl değiştiği P(V)=20.78/V
eşitliği ile daha ayrıntılı olarak gösterilmiştir. Biraz önce basıncın yalnızca
hacmin değil aynı zamanda sıcaklığın ve mol sayısının da fonksiyonu olduğunu
ifade etmiştik. Oysa bu eşitlikte bu sıcaklık ve mol sayısı görülmemektedir.
Bunun nedeni mol sayısı ve sıcaklığın sabir tutulması nedeniyle bu iki
parametrenin 20.78 sabit değeri içinde bulunduğu düşünülebilir. Fakat denel bir
çalışma yapmaksınız sıcaklık ve mol sayısının bu sabit değer içine nasıl
dağıldığını söyleyemeyiz. Benzer
şekilde hacim ve mol sayısı sabit tutularak basınç üzerine sıcaklığın etkisi
P(T) veya sıcaklık ve hacim sabit tutularak basınç üzerine mol sayısının etkisi
incelenebilir P(n). Eğer bu tüm ilişkiler birleştirilirse ideal bir gaz için
eşitliğinin bulunduğu görülebilir . Burada T birimi Kelvin, n birimi mol ve V nin birimi; litredir. Burada da sabit bir değer görülüyor ki bunun genel gaz sabiti olarak adlandırıldığını genel kimya derslerinizden bilirsiniz. Şimdi P nin büyüklüğünü etkileyen başka parametrelerinin olup olmadığını belirlemek isterseniz ne yapabilirsiniz. Yoksa P nin her zaman yukarıdaki eşitliğe uyduğunu düşünmek yeterli midir? Bu şimdilik konumuz dışı olmasına karşın sorunun yanıtını bulmaya çalışın.
Bu kısım boyunca; kimyasal olaylarda etkin olan karşımıza çıkan fonksiyon tipleri ve grafiksel gösterimlerinin nasıl işimize yaradığı üzerinde durulacaktır.
Bu tip fonksiyonların genel gösterim deseni;
y = ax + b
şeklindedir. Buradaki a ve b değerleri sabit sayılardır. Buradaki a değeri grafiğin eğimidir. Eğer a değeri 0 eşitse; fonksiyon değişimi x değerinden bağımsız hale gelir ve x değerlerine karşı y değerleri grafik edilirlerse x eksenine parelel doğrular elde edilir. Eğer a değeri 0 dan küçük ise; bu x değerlerinin artmasıyla birlikte y değerlerinin azalması anlamına gelir ki X= b/a değeri için; Y fonksiyonunun değeri 0 olacaktır. Başka bir uç durum olayı x değeri 0 iken, Y değerinin b ye eşit olması durumudur (Şekil 1) (Örnek 1,).
Eğer bir fonksiyon doğrusal fonksiyon haline getirilebilirse olay üzerinde çalışmak çok kolaylaşır.
![]() tipi fonksiyonlardır.
Bazı adsorpsiyon olaylarını izlemek için bu tip fonksiyonlardan
yararlanılabilir. Örneğin Freundlich adsorbsiyon izoterminde fonksiyon Y=kCn şeklindedir. (Örnek 1,).
tipi fonksiyonlardır.
Bazı adsorpsiyon olaylarını izlemek için bu tip fonksiyonlardan
yararlanılabilir. Örneğin Freundlich adsorbsiyon izoterminde fonksiyon Y=kCn şeklindedir. (Örnek 1,).
Y=ax şeklindeki fonksiyonlardır. Birinci
mertebe reaksiyonlarda konsantrayon değişimi veya radyoaktif bir maddenin
konsantrayon değişimi bu fonksiyona benzer fonksiyona sahiptir (![]() ). Seyreltik çözeltilerden geçen ışığın şiddetinin değişimide
bu fonksiyona benzer(
). Seyreltik çözeltilerden geçen ışığın şiddetinin değişimide
bu fonksiyona benzer(![]() ) (Örnek 1, ).
) (Örnek 1, ).
Çoğu zaman parabolik veya üstel fonksiyonlar ve onların grafikleriyle uğraşmak doğrusal fonksiyonların grafikleriyle uğraşmaktan çok daha zordur. Ayrıca bu tip fonksiyonların değişimlerini daha kolay takip edebilmek için doğrusal hale getirmek oldukça yararlıdır. Yukarıda verilmiş parabolik ve üstel fonksiyonların logaritmik hale hale getirildikten sonraki grafiklerini kontrol edin. (Freundlich Adsorpsiyon İzotermi, C-14 parçalanması)
--------------------------------------
ÖRNEKLER VE ÇÖZÜMLER
Örnek 1: Organik bir madde için 20 ve 50 oC deki ısı kapasitesi Cp sırasıyla 79.619 ve 79.632 J K-1 mol-1 olarak ölçülmüştür. Bu madde için Cp ile sıcaklık arasındaki ilişkinin Cp = a + bT şeklinde olduğu bilindiğine göre fonksiyondaki a ve b değerlerinin değerlerini hesaplayınız.
Çözüm : b değeri ![]() değerine eşit
olacağından
değerine eşit
olacağından
a değeri ise bu fonksiyonda yararlanılarak elde edilebilir.
79.632 J K-1mol-1 = a + (4.33x10-4 J K-1 mol-1)(323.15 K)
a = 79.772 J K-1mol-1
**************
Örnek 1 : Asetik asit çözeltisindeki asetik asitin adsorpsiyonu için Freundlich adsorpsiyon izotermi parametreleri k ve n sırasıyla 2.716 ve 0.432 olarak elde edilmiştir. 0.9 M denge konsantrasyonuna kadar denge konsantrasyonu C ye karşı Y nin değişiminin grafiğini çiziniz.
Çözüm : Çizimi Görmek Tıklayınız.
**************
Örnek 1 : 14C ün parçalanma hız sabiti k = 1.2x10-4 yıl-1 dir. 5000 yıl boyunca 500 yılda bir başlangıçta 1 gram olan 14C ne kadar kalacağını hesaplayarak uygun bir grafik çiziniz.
Çözüm :
Fonksiyon ![]() şeklinde olduğundan
ve
şeklinde olduğundan
ve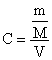 şeklinde gösterilebileceğinden fonksiyon
şeklinde gösterilebileceğinden fonksiyon ![]() şeklinde yeniden
düzenlenebilir.
şeklinde yeniden
düzenlenebilir.
|
t / yıl |
M / g |
|
0 |
1 |
|
500 |
0,9418 |
|
1000 |
0,8869 |
|
1500 |
0,8353 |
|
2000 |
0,7866 |
|
2500 |
0,7408 |
|
3000 |
0,6977 |
|
3500 |
0,6571 |
|
4000 |
0,6188 |
|
4500 |
0,5828 |
|
5000 |
0,5488 |
Fonksiyonun zamanla Değişimi görmek için tıklayın.
--------------------------------------
Bazı
Web Kaynaklar
The Constants and
Equations Pages
Dave's Math Tables: Conic
Sections