Yüzey KimyasıMaddelerin yüzeylerinde fiziksel ve kimyasal olarak meydana gelen olaylarla ilgilenen yüzey kimyası; yüzeylerdeki moleküllerin etkileşimlerini, adsorpsiyonu, katalizini, ıslanmayı, kaplama teknolojilerini ve benzeri konuları inceler. Yüzey kimyası, yüzeylerin özelliklerinin, özellikle de yüzey alanı, yüzey morfolojisi, yüzey yükü, yüzey potansiyeli, yüzey enerjisi gibi faktörlerin, birçok kimyasal ve fiziksel özellikler üzerindeki etkisini de incelemektedir. Yüzeylerin özellikleri, birçok endüstriyel ve biyolojik uygulama için son derece önemlidir. Endüstriye uygulamalara örnek olarak;
Biyolojik uygulamalara örnek olarak;
Yüzey kimyası, fiziksel kimya, malzeme bilimi, yüzey bilimi, kimya mühendisliği, biyoloji ve diğer birçok disiplinle ilgili olduğu için, çok yönlü bir disiplindir. Bir malzemenin yüzeyindeki fonksiyonel grupların sayısı ve polaritesi, yüzeyin hidrofobisitesi veya hidrofilisitesi gibi faktörleri etkileyebilir. Bu faktörler, malzemenin yüzey enerjisi seviyesini belirleyebilir ve bu da malzemenin özelliklerini etkiler. Örneğin, bir malzemenin yüzeyi daha polar hale geldiğinde, yüzey enerjisi artar ve malzeme daha kolay ıslanabilir hale gelir. Bununla birlikte, bir malzemenin yüzeyi daha hidrofobik hale geldiğinde, yüzey enerjisi azalır ve malzeme daha az ıslanabilir hale gelir. Yüzey enerjisinin büyüklüğü malzemenin ıslanabilirliği, yapışma ve diğer yüzey özelliklerini etkiler. Yüzey kimyası, bir sıvının yüzeyindeki moleküllerin etkileşimlerini inceledeğinden yüzey gerilimini hakkında bilgi verir. Örneğin, bir yüzeyin polaritesi, yüzey gerilimini etkileyebilir çünkü polar moleküller birbirlerine daha çok çekilirler ve daha yüksek bir yüzey gerilimine neden olurlar. Benzer şekilde, bir yüzeyin hidrofobisitesi (su iticiliği) de yüzey gerilimini etkileyebilir çünkü hidrofobik yüzeyler daha düşük yüzey gerilimine sahip olabilirler. Dolayısıyla, yüzey kimyası ve yüzey gerilimi arasında yakın bir ilişki vardır ve yüzey kimyası, yüzey gerilimini etkileyebilecek faktörleri inceleyerek yüzey gerilimini kontrol etmeye yardımcı olur. Saf Maddelerin Arayüzey Gerilimi Arayüzey gerilimi, bir sıvı veya gazın yüzeyindeki moleküller arasındaki çekim kuvvetlerinden kaynaklanan gerilimdir. Katı yada sıvı yüzeyleri anizotropik davranış gösterir. Beş tür arayüzeyden söz edilebilir. Bunlar; katı-katı, katı-sıvı, katı-gaz, sıvı-sıvı, sıvi-gaz temas alanlarıdır. Heterojen sistemlerdeki hemen tüm etkileşmelerin bu yüzeylerde başladığı düşünülürse, yüzey kimyasının ne kadar geniş ve önemli bir alanı elinde tuttuğu kolayca kavranabilir.
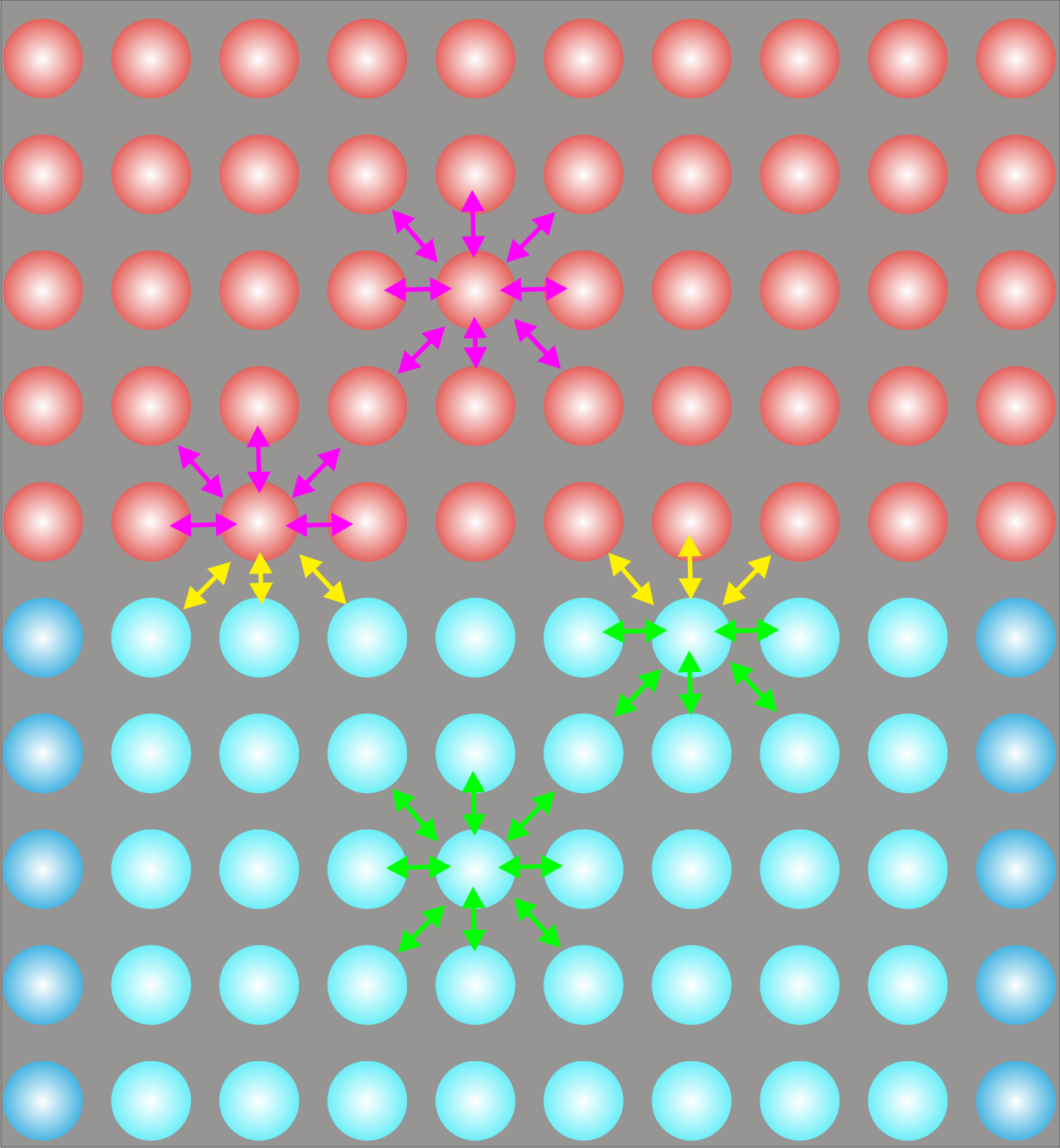
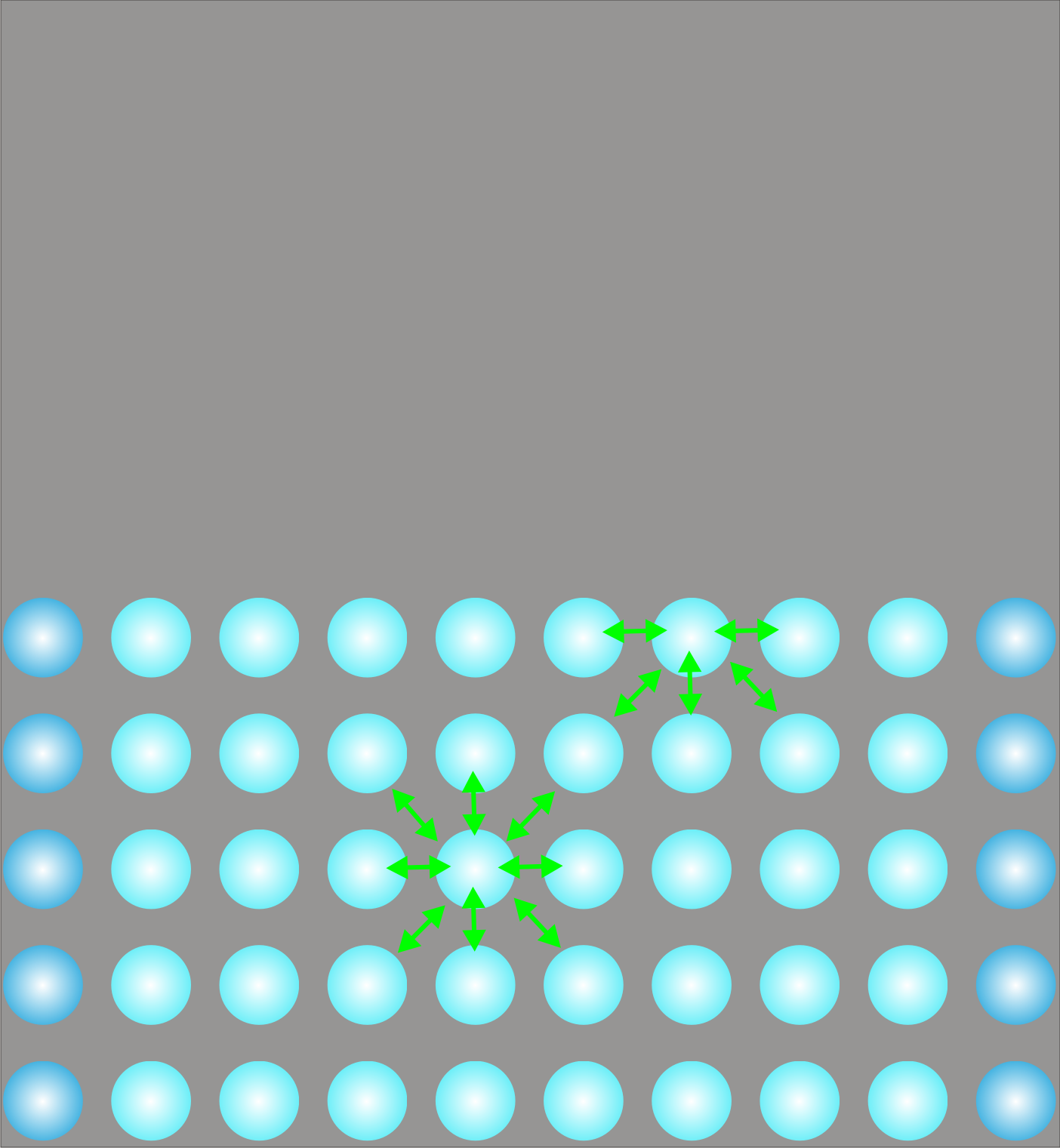
Bir katı veya sıvının yüzeyindeki moleküller, iç kısımlarındaki moleküllerden farklı bir çevreye sahiptirler. Bu farklılığın nedeni etraflarındaki komşu moleküllerin farklılıklarının bir sonucudur. Şekil 1 de görüldüğü gibi farklı moleküllerin kohezyon kuvvetleri birbirinden farklıyken (yeşil ve eflatun oklarla gösterilmiştir.), farklı moleküler arasında meydana gelen adezyon kuvvetleri de farklıdır (sarı oklar ile gösterilmiştir.) Eğer ikinci bir molekül katmanı yoksa veya ikinci faz çok seyreltikse (örneğin gaz ise) yüzeydeki moleküller arasındaki daha belirgin olarak ortaya çıkacaktır (Şekil 1 deki resime tıklayın.). Moleküller arasındaki kohezyon kuvvetleri adezyon kuvvetlerinden fazlaysa, veya pratik olarak adezyon kuvveti yoksa yüzeydeki molekülleri içeri çekmek için net bir kuvvet oluşturur. Bu nedenle; bu kuvvet yüzey alanını en küçük şekle sokmaya zorlar. Maddenin kararlı hallerinde doüru gidilirken enerji düşmesi gerektiğinden maddenin iç kısımlarına göre yüzeyde bir enerji fazla olması gerektiği sonucu ortaya çıkar. Başka bir değişle, moleküllerin ne kadarı iç kısımlarda bulunursa diğer moleküller ile o kadar iyi etkileştiklerinden yüzey küçülmesi ile enerji azalması meydana gelecektir. Bu durumda; bir maddenin yüzeyini büyütebilmek için enerjiye ihtiyaç olacaktır. Bu büyüklük genellikle \rm cm^2 başına erg veya cm başına dyn olarak verilir. Örneğin Örneğin; suyun yüzey gerilimi 20 \rm ^oC de 72.8 dyn \rm cm^{-1} veya 72.8 erg \rm cm^{-2} olduğundan suyun yüzeyinde 20 \rm ^oC de 1 cm lik bir çizik oluşturabilmek için 72.8 dyn e veya aynı sıcaklıkta suyun yüzeyini 1 \rm cm^{-2} genişletebilmek için 72.8 erg lik bir enerjiye ihtiyaç vardır. Bazı sıvıların yüzey gerilimi Tablo 1 de gösterilmiştir. Benzer şeyler katı bir madde içinde söylenebilir. Fakat katı maddeleri için yüzey gerilimi yerine yüzde tutma ya da yüzey aktifliği terimleri kullanılır. Katıların yüzey aktivitesi; özellikle katı çok iyi bir şekilde bölündüğünde gaz adsorpsiyonu meydana gelmesiyle görülür ki bu pekçok kimyasal reaksiyonu katalizlemek için kullanılan heterojen katalizör sistemleriyle sıkı sıkıya ilişkilidir. Sıvıların yüzey gerilimi sıcaklığın artmasıyla azalır (Tablo 1). Eğer sıvının sıcaklığı sürekli arttırılacak olursa yüzey geriliminin sıvının kritik sıcaklığına ulaşmadan önce sıfır olduğu görülür. W.Ramsay ve J. Shields yaptıkları geniş sıcaklık aralıklarında yaptıkları çalışmalar sonucu yüzey geriliminin sıcaklıkla değişmesine ilişkin \rm \gamma \Big( { M \over d} \Big ) ^{2/3} = k(t_k \; - \; \delta \; - t ) \qquad \qquad (Eşitlik \; 1)
emprik eşitliğini türettiler. Burada \rm \gamma; sıvının yüzey gerilimi, M; mol tartısı, d; sıvının yoğunluğu, k; Eösvös sabiti ( \rm 2.1 \times 10^{-7} J K^{-1} mol^{-2/3}) , \rm t_k; kritik sıcaklık, \rm \delta; sıvının doğansına bağlı ve genellikle 6 olan sabit bir sayıdır. Eğer bir sıvı için \rm \delta=6 ise sıvının kritik sıcaklığına ulaşmadan 6 \rm ^oC yüzey gerilimi sıfır olur demektir.
Şekil 1 de görüldüğü gibi iki sıvı birbiri ile temasta bulunuyorsa, aralarındaki yüzey ne birinci ne de ikinci sıvıya benzemez. Bu iki sıvının arasındaki bu alan sıvıların arayüzeyleridir. Eğer A ve B gibi iki sıvıdan bahsedildiğinde arayüzey gerilimi \rm _A \gamma _B şeklinde gösterilir. Bu alanda A ve nin molekülleri etkileşeceklerinden arayüze gerilimi her iki sıvının yüzey geriliminden daha küçük değerdedir. Bu büyüklük için G.N. Antanow tarafından önerilmiş Antonow Yaklaşık Bağıntısı kullanılır. \rm \rm _A \gamma _B = \gamma _A - \gamma _B
Burada \rm \gamma _A > \gamma _B dir. Ancak unutulmamalıdır ki iki sıvı arasındaki moleküler etkileşmeler yüksek ise arayüzey gerilimi bu bağıntı ile beklenenden çok daha düşük olur. İfadeden de görüldüğü gibi sıvıların herbirinin ayrı ayrı yüzey gerilimleri toplamı bu İki sıvının oluşturduğu arayüzey gerilimlerinden herzaman daha büyüktür ( \rm _A \gamma _B < \gamma _A - \gamma _B ). İki sıvının bir arayüzey oluşturmak üzere bir araya gelmesi ile toplam yüzey serbest enerjisinde azalma meydana geleceğinden bu sıvıları birbirinden ayırmak içinde bir iş yapmak gerekir. Bu işin büyüklüğü, \rm W_a \rm W_a = \gamma _A + \gamma _B - _A \gamma _B \qquad \qquad (Eşitlik \; 2)
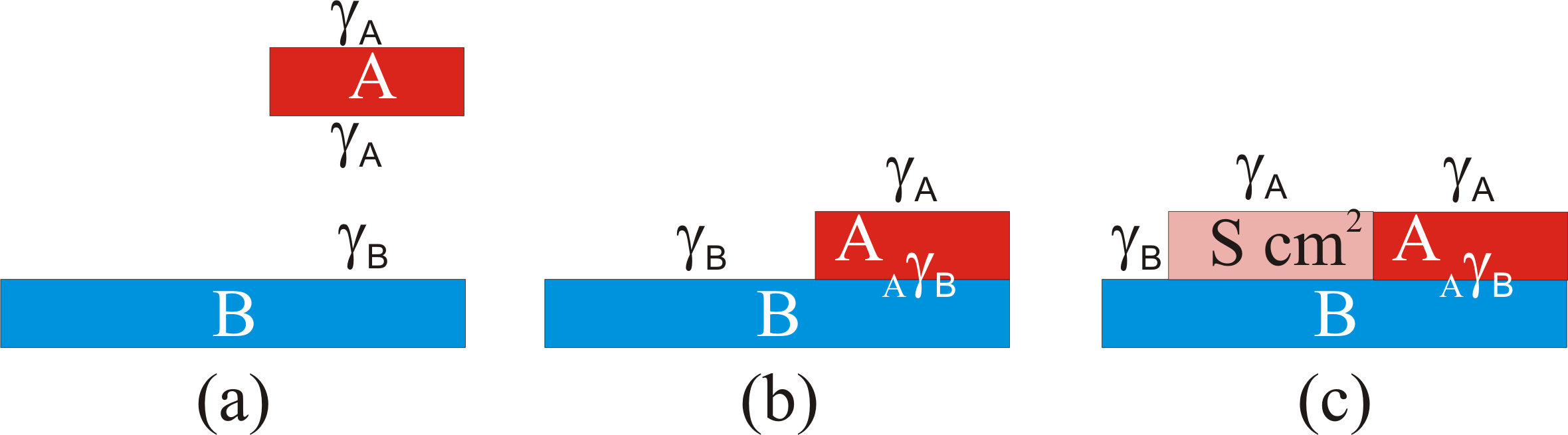
olup adezyon işi olarak adlandırılır. Bu olay Şekil 2 - (a) Şekil 2 - (b) de gösterilmiştir. Eğer A ve B sıvıları aynı sıvılarsa bu kez yapılması gereken iş kohezyon işi, \rm W_k , olarak adlandırılır ve \rm W_k=2 \gamma _A \qquad \qquad (Eşitlik \; 3)
eşitliği ile verilir. Zaten herhangi bir arayüzey oluşumu söz konusu olamaz.
Bundan sonra ilginç olan sorulardan biri B sıvısı üzerine konan A sıvısının B sıvısı üzerinde yayılıp yayılmayacağı sorusudur. Bu durumda \rm cm^2 başına artan ya da azalan enerjinin ne kadar olduğunu belirlemeye çalışalım. Başlangıçta A sıvısının yayılacağı yüzey üzerinde yalnızca B sıvısının yüzey gerilimi, \rm \gamma _B söz konusuyken, A sıvısı yayıldıktan sonra bunun yerini A sıvısının yüzey gerilimi \rm \gamma _A ve A-B sıvıları arasındaki arayüzey gerilimi \rm _A \gamma _B alacaktır. O halde \rm cm^2 başına değişen enerji büyüklüğü \rm \Delta E = \gamma _B - \big( _A \gamma _B + \gamma _A \big) \qquad \qquad (Eşitlik \; 4)
olacaktır. Eğer \rm \gamma _B < _A \gamma _B + \gamma _A ise; A sıvısı B üzerinde yayılmayacaktır. tersi durumda, yani \rm \gamma _B > _A \gamma _B + \gamma _A ise A sıvı B sıvısı üzerinde yayılacaktır. Bir başka deyişle; \rm \Delta E nin sayısal değeri sıfırdan küçükse, A sıvısı B sıvısı üzerinde yayılmaz, sıfırdan büyükse yayılabilir demektir. Çözeltilerin Yüzey Gerilimleri : Bir çözücü içerisinde bir madde çözündüğünde çözeltinin yüzeyindeki moleküler etkileşmeler değişeceğinden saf çözücünün yüzey gerilimine göre değişiklik olmalıdır. Sabit bir sıcaklıkta bu değişikliklerin büyüklüğü madde tipine ve konsantrasyona bağlı olarak değişim gösterir.
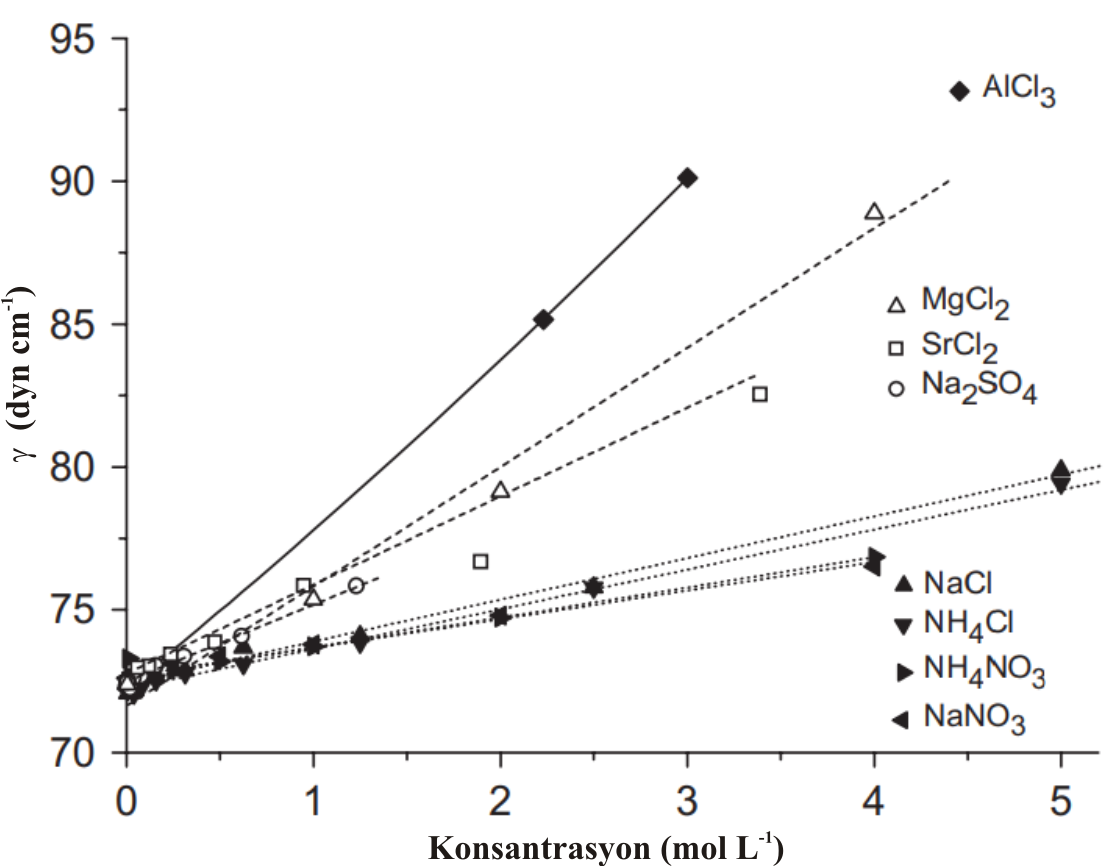
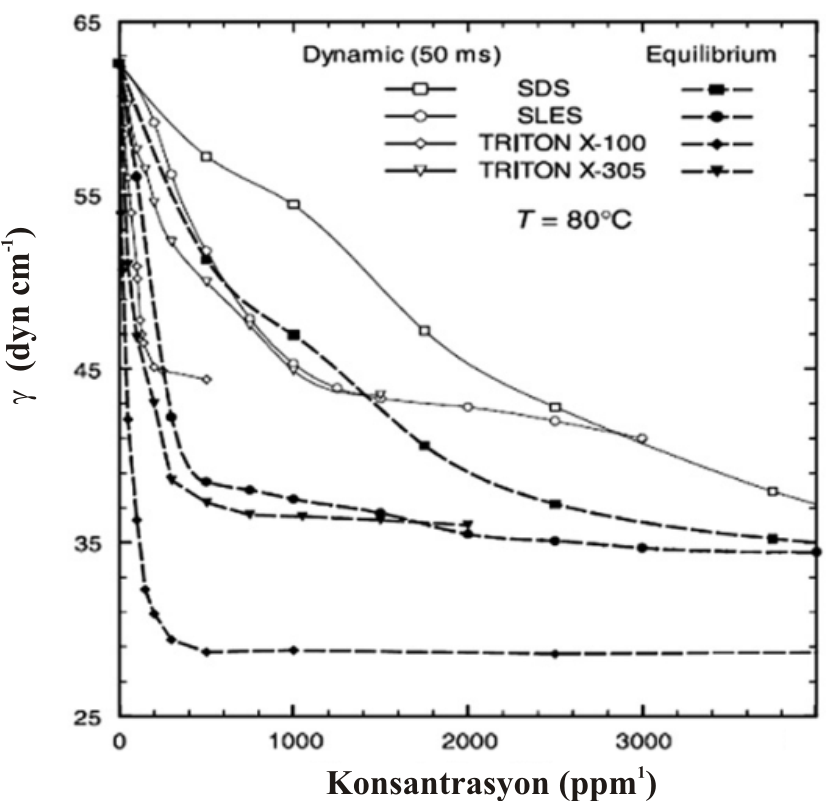
Çeşitli çözeltileri hazırlamak için kullandığımız suyun yüzey gerilimi moleküler arasındaki hidrojen bağları nedeni ile yüksektir. Genellikle inorganik tuz çözeltileri hazırlandığında, su moleküllerinin yüzeyde iyonik etkileşmeler ile yüzey gerilimi daha da artarken , çeşitli sabun çözeltileri hazırlanması sırasında oldukça düşük değerlere ulaşır (Şekil 3).
Saf bir madde içerisinde, bir madde çözünüyorsa çözünen maddenin ve çözücünün karakterine bağlı olarak yüzey geriliminin değiştiği gözlenmiştir. Ayrıca yapılan incelemelerle, çözünen maddenin, sıvının İç kısımlarındaki konsantrasyonu ile yüzeydeki konsantrasyonlarının - birbirinden farklı olduğu gözlenmiştir ki bu beklenen bir olaydır. Termodinamik düşüncelerle Gibbs; \rm \Gamma = - { C \over RT } { d \gamma \over dC } \qquad \qquad (Eşitlik \; 5)
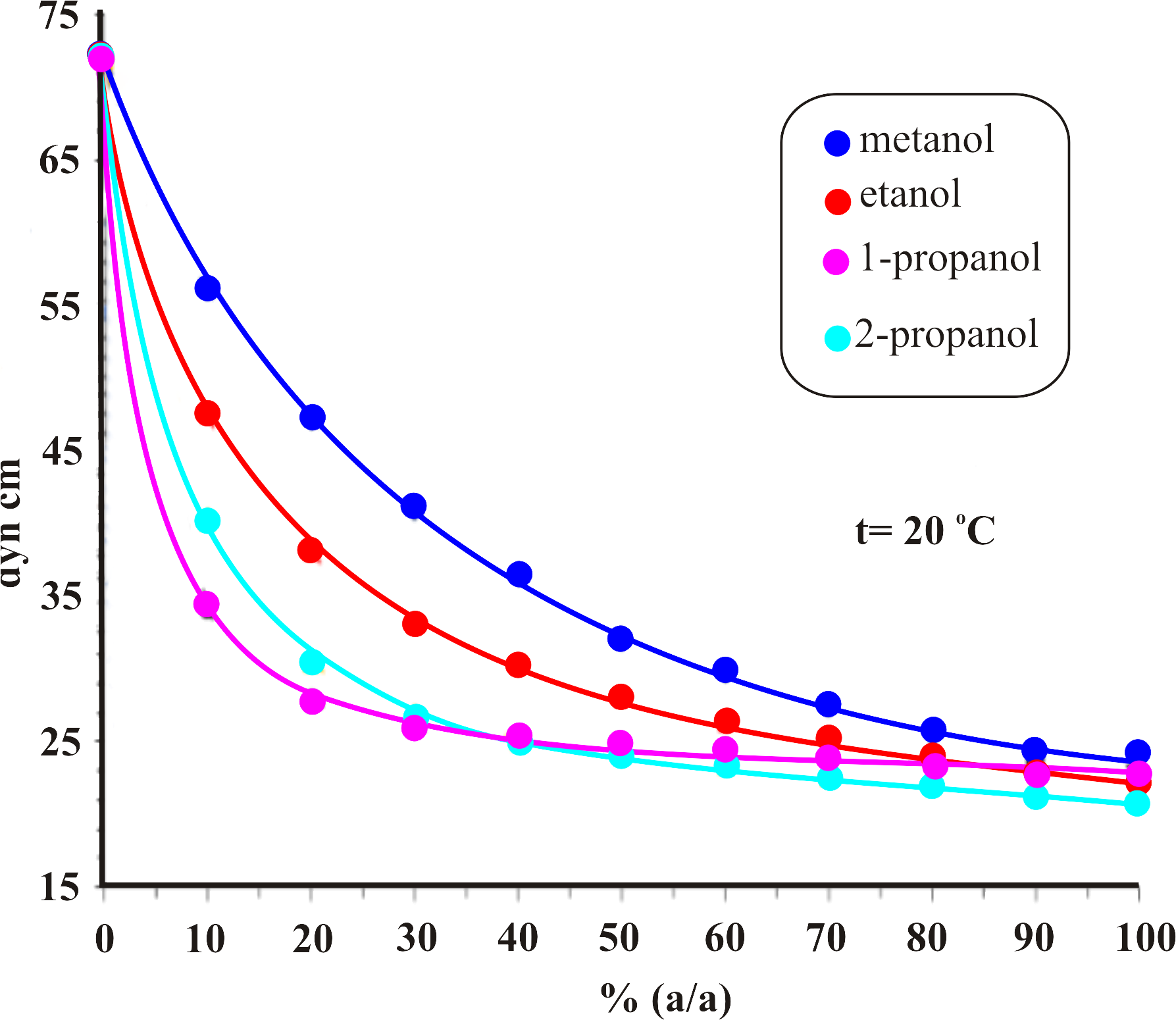
\rm \Gamma ; yüzeyin \rm cm^2 sinde bulunan çözünmüş madde miktarının çözeltinin iç kısımlarına göre fazlalığını veya eksikliğini gösterir. Burada, \rm \Gamma C konsantrasyonu için \rm { d \gamma \over dC } değişimi yardımı ile hesaplanır. Değişen konsantrasyon ile birlikte \rm \Gamma değerleri de değişecektir. Şekil 3 ve Şekil 4 de görülen grafikler yardımı ile çözünen türlerin için çeşitli konsantrasyonları için \rm \Gamma değerleri hesaplanabilir. Eğer bir maddenin konsantrasyonu, çözeltinin iç kısımlarına göre yüzeyde daha fazla ise; bu tür maddeler kapiler aktif, çözeltinin iç kısımlarına göre yüzeydeki konsantrasyon daha az ise bu tür maddeler de kapiler İnaktif olarak adlandırılır. Kapiler aktif madde çözetileri için Szyskowski tarafından \rm \gamma = \gamma _o - a log (1+bC) \qquad \qquad (Eşitlik \; 6)
bağıntısı verilmiştir. Burada \rm \gamma _o; saf çözücünün yüzey gerilimi, \rm \gamma ; C konsantrasyonundaki çözeltinin yüzey gerilimidir. a ve b maddeye özgü sabit değerlerdir. Kapiler inaktif maddeler için çözeltilerinin yüzey gerilimleri \rm { \gamma - \gamma _o \over \gamma _o } = m C \qquad \qquad (Eşitlik \; 7)
eşitliği geçerlidir. Uygun bir şekilde çizilen grafikten m değeri hesaplanarak katyon ve anyonların inaktiflik dereceleri birbirlerine göre düzenlenebilir. Yüzey ve Arayüzey Gerilimlerinin Ölçülmessi : Yüzey ve arayüzey gerilim büyüklüklerini belirleyebilmek için pek çok yöntem geliştirilmiştir. Bu yöntemler statik ve dinamik yöntemler olmak üzere İki grup altında toplanabilir. Statik yöntemler belirli bir zaman aralığında değişmeden kalan ve sıvının içi kısmıyla dengede olan bir yüzeyin yüzey gerilimini ölçme yöntemi olarak kullanılır. Dinamik yöntemler genişlemekte ya da daralmakta olan ve henüz dengeye gelmemiş yüzeylerin yüzey gerilimlerini ölçmek için gibi yöntemleri kullanılır.
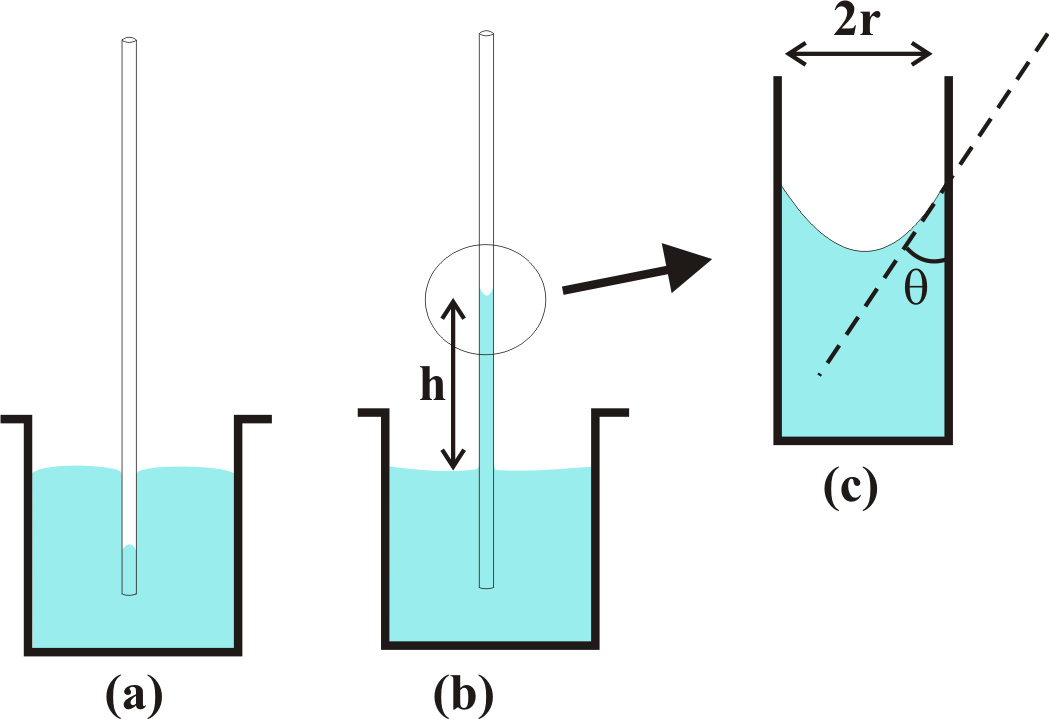
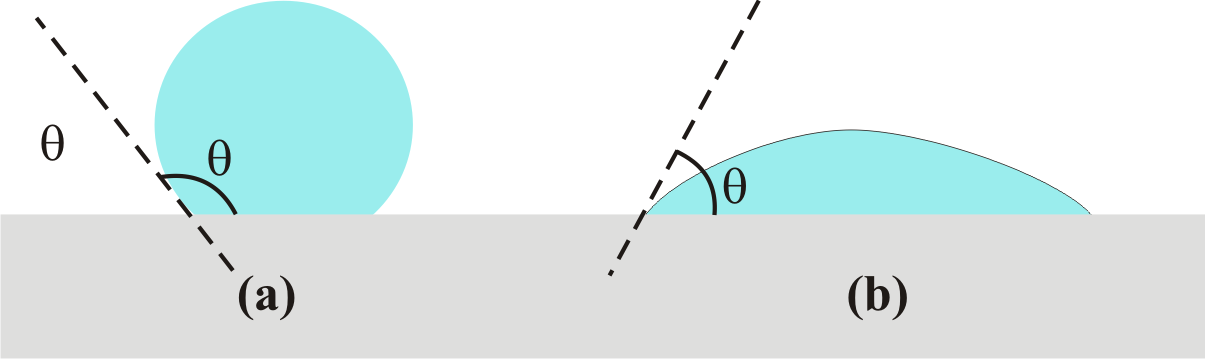
Kapiler Yükselme Yöntemi : Bir sıvının bulunduğu kabın cidar ile temasta bulunan moleküller yukarıda da bahsedildiği gibi adezyon kuvvetlerinin etkisi altındadır. Bu nedenle sıvı yüzeyi kabın cidarına dik durumda bulunmaz. Bu durum Şekil 5 de gösterilmiştir. Bu eğriliğin nedeni adezyon kuvvetlerinin yanısıra, kabın cidarında bulunan bir molekülün kohezyon ve yerçekimi kuvvetlerinin etkisi altında olmasından kaynaklanır. Fakat molekülün kütlesi hesaba katılacak olursa, yerçekimi etkisinin diğer iki kuvvet yanında kolayca ihmal edilebilir . Bu iki kuvvet bileşkesine bağlı olarak sıvı İç bükey ( bu durumda adezyon kuvvetleri - kohezyon kuvvetlerinden daha büyük ) (Şekil 5 b) ya da dış bükey ( bu durumda kohezyon kuvvetleri adezyon kuvvetlerinden daha büyük ) (Şekil 3 a) bir durumda bulunabilir. Sıvıyla cidar arasındaki açı her iki kuvvetten hangisinin daha üstün olduğunu gösterir. Bu durumlar Şekil 6 de gösterilmiştir. Eğer sıvının katı ile yaptığı \rm \theta açısı 90 dereceden daha küçükse, sıvı katıyı ıstatabilir ( Şekil 6 b ). Eğer açı 90 dereceden daha büyükse sıvı katıyı ıslatmaz ( Şekil 6 a ).
Eğer yarıçapı (r) yeterince küçük bir kapilerin iç yüzeyini tamamen ıslatabilen bir sıvı içine daldırıldığını ve kapiler duvarının ince bir film adsorpladığını düşünürsek sıvının yükselmesi ile kapilerin içindeki yüzey alanının azalması ile toplam yüzey enerjisinde bir azalma meydana gelecektir. Şekil 5 b deki silindirik kapiler içinde dh kadar yükselmesi ile kapiler cıdarındaki yüzey enerjisi azalması \rm \gamma 2 \pi rdh olurken kapiler içindeki sıvının hacim artışı \rm 2 \pi r ^2 dh kadar olacaktır. Bu durumda sıvının dh kadar yükselmesi ile yüzey serbest enerjisindeki düşme \rm dG; \rm dG_y = \gamma dA = \gamma 2 \pi r dh
olurken, yerçekimi ivmesinin g olduğu bir yerde \rm \rho yoğunluğundaki sıvının yerçekimine karşı dh kadar yükselmesi ile h yüksekliğinde serbest enerjisindeki artış \rm dG_a; \rm dG_a = \pi r ^2 \rho g h dh
olacaktır. Sistem dengeye gelene kadar sıvı kapiler içinde yükselmeye devam edecektir. İki serbest enerji birbirine eşit olduğunda sıvının yükselmesi duracaktır ( \rm dG_y = dG_a ). Bu durumda yüzey gerilimi \rm \gamma için; \rm \gamma = { r \rho g h \over 2 } \qquad \qquad (Eşitlik \; 8)
eşitliği elde edilir. Eşitliğin sağ tarafındaki büyüklükler ölçülebildiğinden yüzey gerilim büyüklüğü hesaplanabilir. Bu eşitlik sıvının tamamiyle camı ıslattığı kabul edilerek çıkartılmıştır. Camı tamamen ıslatmayan sıvılar için ise cam-sıvı arasındaki \rm \theta açısına bağlı olarak \rm \gamma = { r \rho g h \over 2 } cos( \theta ) \qquad \qquad (Eşitlik \; 9)
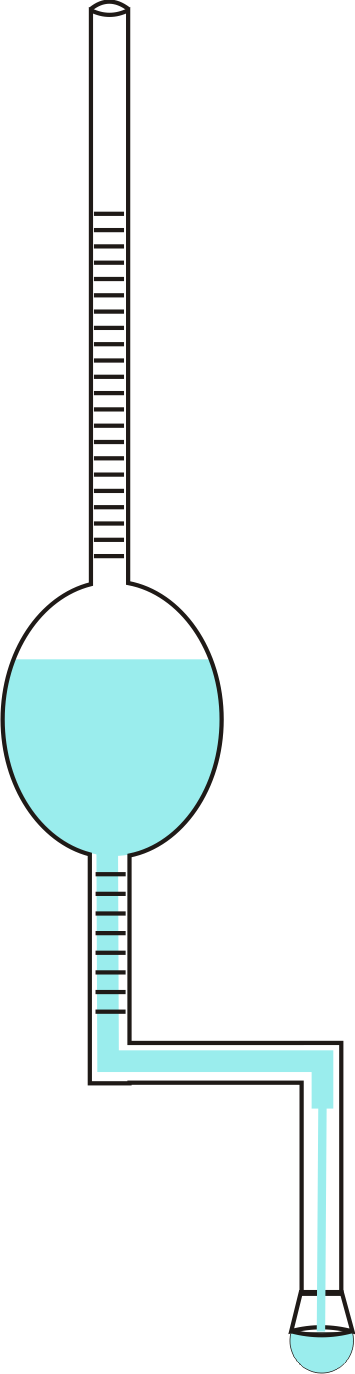
eşitliği ile bulunur. Damla Ağırlığı Yöntemi : Bu yöntemde yüzey gerilimini belirlemek için Şekil 7 deki Traube Stalogmometresi kullanılır. Bu metoda göre; kılcal bir borudan düşen damlanın ağırlığı, kütlesi m ve yerçekim ivmesi g ye bağlı olmak üzer tam düşme anında borunun çevresindeki sıvının yüzey gerilim kuvvetine eşit olacaktır ( \rm 2 \pi r = mg ). Bu eşitlikten yüzey gerilimi hesaplanabilir.
Fakat damlanın düşüş anı fotoğrafları incelendiğinde , damlanın boru ile sıvının tam birleştiği yerden kopmadığı, düşen damla ile boru ucu arasında bir miktar sıvı kaldığı gözlenmiştir. Bu nedenle, yapılan araştırmalarla yukarıdaki bağıntı yerine \rm \gamma = F {mg \over r}
eşitliğinin daha geçerli olduğunu göstermiştir. Buradaki F değeri; damlanın hacmi \rm \upsilon olmak üzere, \rm r / \upsilon ^{1/3} terimi ile orantılı olduğu görülmüştür. Tablo 1 de \rm r / \upsilon ^{1/3} değerlerine göre değişen düzeltme föktörü F değerleri verilmiştir. Sabit hacimde bir sıvının yüzey gerilimini Traube stalogmometresi ile ölçmek için, belli hacimde sıvı stalogmometreye alınarak ucundan serbest düşmeye bırakılır ve düşen damlalar sayılır. Eğer aynı hacimde verilen bir karşılaştırma sıvısı ile deneme yapılırsa, bilinmeyen sıvının yüzey gerilimi F faktörleri birbirine eşit kabul edilerek \rm \gamma _{bilinmeyen} = \gamma _{referans} { n _ {referans} d_{bilinmeyen} \over n _ {bilinmeyen} d_{referans}} \qquad \qquad ( Eşitlik \; 10)
eşitliğinden hesaplanabilir. Burada \rm n _ {referans}; yüzey gerilimi bilinen referans maddenin stalogmometreden koparak düşen damla sayısı, \rm n _ {bilinmeyen}; yüzey gerilimi hesaplanacak maddenin stalogmometreden koparak düşen damla sayısı, \rm d _ {referans}; referans maddenin çalışılan sıcaklıktaki yoğunluğu \rm d _ {bilinmeyen}; yüzey gerilimi hesaplanacak maddenin çalışılan sıcaklıktaki yoğunluğudur.
Halka Koparma Yöntemi : Bu yöntem kullanılarak yüzey ve arayüzey gerilimleri ölçülebilir. Bu yöntem ile yüzey gerilimi ölçek için kullanılan bir cihazın resmi Şekil 8 de verilmiştir. Sabit temas açısının korunması için sıvıya daldırılan platin halkalar uygun br yöntem ile temizlenir. Telin kopma kuvveti ile yüzey veya iki farklı sıvının arasında ortaya çıkan arayüzey gerilimi hesaplanabilir.
Kaynaklar
https://www.jlabexport.com/tension-coefficients-apparatus (10.04.2023) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||