Newton Soğuma Yasası Newton Soğuma Yasası, İngiliz fizikçi ve matematikçi Isaac Newton tarafından 1701 yılında keşfedilmiş bir kuraldır. Kural, daha sonra termodinamiğin önemli kurallarından biri olarak kabul edilmeye başlandı ve günümüzde de hala yaygın olarak kullanılmaktadır. Sıcaklığı yüksek olan bir sistem daha düşük sıcaklıktaki bir ortamda zamanla kendiliğinden soğur. Soğuyan sisteme göre çok büyük olan ortamın sıcaklığındaki değişim ihmal edilebilecek kadar küçük kalmaktadır. Sistemin sıcaklığının zamanla değişim hızı olarak tanımlanan soğuma hızı Newton Yasasına göre sistem ile ortam arasındaki sıcaklık farklı ile doğru orantılıdır. Sistemin başlangıçtaki ve herhangi bir andaki sıcaklıkları sırası ile \rm T_o ve T ile ortamın sabit kaldığı varsayılan sıcaklığı \rm T_{ort} ile simgelendiğinde k orantı sabiti olmak üzere Newton Denklemi; \rm - { dT \over dt} = k(T-T_{ort}) şeklinde yazılır. Zaman artarken sistemin sıcaklığı düştüğünden dolayı eşitliğin sol tarafına - işareti konulmuştur. 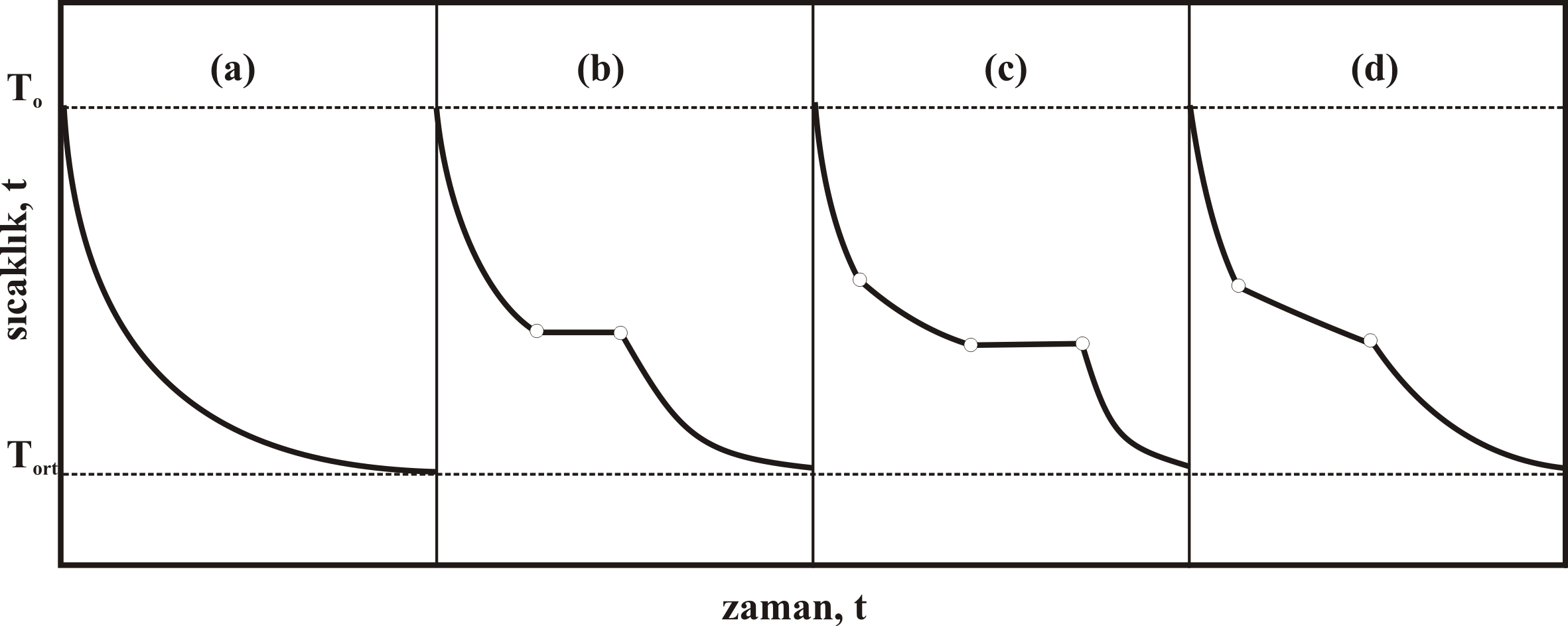Soğuma süresi sıfırdan t ye kadar artarken sistemin sıcaklığı \rm T_o dan T ye kadar düşeceğinden \rm \int _{ T_o} ^T { dT\over T - T_{ort}} = - k \int _0 ^t dt \rm ln{ T - T_{ort} \over T_o -T_{ort}} = -kt \qquad \qquad \qquad \text{(Eşitlik - 1)} \rm T=T_{ort} + (T_o - T_{ort} )e^{-kt} \qquad \qquad \qquad \text{(Eşitlik - 2)} eşitliği bulunur. Bu eşitliğe göre; soğuyan sistemin sıcaklığı zamanla üstel olarak düşmektedir. Soğuma zamanı sonsuza giderken sistemin sıcaklığı da ortamın sıcaklığına ulaşmaktadır. Bazı sistemlerin soğuma eğrileri Şekil 1 de gösterilmiştir. Bu tür grafikler soğuyan bir sistemin faz diyagramlarının ayrıntılı şekilde çizilmesinde yardımcı olur. Eşitlik 1 den görüldüğü gibi t ye karşı \rm ln{ T - T_{ort} \over T_o -T_{ort}} çizilen doğrunun eğiminden k değeri hesaplanabilir. Şekil 1 : (a) Bir maddenin soğuma eğrileri. (a) faz dönüşümü olmayan bir sistemin soğuma eğrisi. (b) soğuma sırasında tamamen donan bir sistemin soğuma eğrisi. (c) soğuma sırasında önce kısmen kristallenen sonra da tamamen kristallenmenin gelenbir sistemin soğuma eğrisi. (d) kısmen kristallenme ile donan bir sistemin soğuma eğrisi. Newton Soğuma Yasasının Bazı Uygulamaları Newton soğuma kanuna adli tıpta, cesedin sıcaklığı ile olay yeri sıcaklığı arasındaki fark Newton Soğuma Yasasına uygulanarak olayın gerçekleştiği zaman hesaplanabilir. Buzdolabından çıkartılan bir suyun veya sıcak bir maddenin oda sıcaklığına ulaşma zamanı hesaplanabilir. Aşırı yüksek sıcaklık nedeni ile sıcaklığı ölçülemeyen bir maddenin sıcaklığı ölçülebilir değerlere ulaştığında ilk sıcaklığı bu yasaya göre hesaplanabilir. Sıcaklığı öl Dondurma dondurucudan çıkarıldığında erimeye başlar. Dondurmayı eritmek için gereken süre, Newton'un soğuma kanunu uygulanmadan hesaplanamaz. Dondurmanın sıcaklığı ile çevre sıcaklığı arasındaki fark bilindiği takdirde, dondurmanın erime hızı kolaylıkla hesaplanabilir. Bu, dondurma satıcılarının ve distribütörlerinin yeterli sıcaklığı hesaplamalarına ve ürünleri için depolama tesislerini uygun şekilde düzenlemelerine yardımcı olur.