İdeal Çözeltilerin Buhar Basınçları
Birbiri ile homojen olarak karışabilen ve ideal davranış gösteren bir çözelti sisteminde
herbir bileşen ideal davranış göstereceğinden \rm a_1 = \chi _1 ve \rm a_2 = \chi _2
yazılabilir. Çözeltideki herhangi bir bileşenin aktifliği, \rm P_i; çözeltideki i bileşeninin kısmi basıncı ve \rm P_i ^o; i bileşeninin saf haldeki buhar basıncı olmak üzere \rm a_i = P_i / P_i^o olacağından iki bileşenin ayrı ayrı buhar basınçlar için;
\rm p_1= \chi _1 P_1 ^o \qquad p_2= \chi _2 P_2 ^o
yazılabilir. Bu eşitlik Raoult Kanunu'nun matematiksel ifadesidir.
Raoult Kanunu; çözücü içindeki uçucu bileşenin kısmi buhar basıncı, bileşenin saf halinin buhar basıncı ile çözelti içindeki mol kesrinin çarpımına eşittir.
Çözeltinin toplam buhar basıncı;
\rm P_T = P_1 + P_2
\rm P_T = P_1^o \chi _1 + P_2^o \chi _2
\rm \chi _1 + \chi _2 = 1 olduğundan;
\rm P_T = P_1^o \big( 1 - \chi _2 \big) + P_2^o \chi _2
\rm P_T = \big( P_2^o - P_1^o \big) \chi _2 + P _1 ^o
elde edilir. Belli bir sıcaklık için \rm P_1^o \; ve \; P_2^o sabit olacağından
\rm \chi _2 ye karşı \rm P _T değişimi doğrusaldır. Ayrıca \rm \chi _2 = 0 için \rm P _1 ^o
değeri ele geçer. \rm \chi _2 = 1 için \rm P _2 ^o değerine ulaşılır (Şekil 1-a).
|
|
|
| (a) | (b) |
|
Şekil 1 : Sabit sıcaklıkta
(a) iki bileşenli sistemde her iki bileşenin kısmi buhar basınçlarının ve toplam basıncın bileşenlerden birinin mol kesri ile değişimi.
(b) iki bileşenli sistemde mol kesri ile toplam buhar basıncının ve destilatın toplam buhar basıncının değişimi.
|
Çözeltideki bileşenlerin buhar fazındaki kısmi basınçları bilindiğinden, buhar fazındaki herbir bileşenin mol kesri de Dalton Kısmi Basınçlar Yasasına göre bellidir. Örneğin ikinci bileşenin buhar fazındaki mol kesri
\rm Y_2= {P_2 \over P_T}
eşitliği yazılabilir. \rm P_2 \; ve \; P_T değeri yerine konulursa;
\rm Y_2= {P_2 ^o \chi _2 \over \big( P_2 ^o - P_1 ^o \big) \chi _2 + P_1 ^o }
ifadesi elde edilebilir. \rm P_1 ^o \neq P_2 ^o olduğu durumlarda \rm Y_2 \neq \chi _2
olup çözelti bileşeninin buhar fazındaki mol kesri son eşitlik yardımı ile hesaplanabilir.
Şekil 1-b de sabit sıcaklıktaki çözeltinin sıvı ve buhar fazlarına ait buhar basıncı değişimi görülmektedir.
Şekil 1-b herhangi bir \rm \chi _2 bileşimindeki buhar fazı yoğunlaştırılırsa \rm Y _2 bileşiminde
bir öncekine göre farklı bileşimde bir karışım ele geçecektir.
Elde edilen \rm Y _2 bileşimindeki bu karışımın buharları yeniden yoğunlaştırılırsa yeni bileşimde bir karışım elde edilir.
İşlem tekrarlanarak daha zenginleşmiş karışımlar elde edilebilir.
Yukarıdaki \rm P_1 ^o = 25 mmHg ve \rm P_2 ^o = 100 mmHg sistemi için hesaplama yapalım. Aşağıdaki hesaplamayı yapalım.
\rm X_2 = 0.2 için;
\rm P_2 = P_2 ^o \chi _2 = (100 \; mmHg)(0.2) = 20 \; mmHg
\rm P_T = \big( P_2 ^o - P_1 ^o \big) \chi _2 + P_1 ^o = \big( 100 \; mmHg \; - \; 25 \; mmHg \big) 0.2 + 25 \; mmHg =40 \; mmHg
\rm Y_2 = { P_2 \over P_T } = { 20 \over 40 } = 0.5
Görüldüğü gibi 2. bileşenin mol kesri karışımda 0.2 iken buhar fazında 0.5 dir.
0.5 bileşimindeki buhar yoğunlaştırılmış olsa ve yeniden buhar fazındaki bileşime bakılırsa;
\rm P_2 = P_2 ^o \chi _2 = (100 \; mmHg)(0.5) = 50 \; mmHg
\rm P_T = \big( P_2 ^o - P_1 ^o \big) \chi _2 + P_1 ^o = \big( 100 \; mmHg \; - \; 25 \; mmHg \big) 0.5 + 25 \; mmHg =62.5 \; mmHg
\rm Y_3 = { P_2 \over P_T } = { 50 \over 62.5 } = 0.8
elde edilir. İşlem benzer şekilde tekrarlanırsa
\rm P_2 = P_2 ^o \chi _2 = (100 \; mmHg)(0.8) = 80 \; mmHg
\rm P_T = \big( P_2 ^o - P_1 ^o \big) \chi _2 + P_1 ^o = \big( 100 \; mmHg \; - \; 25 \; mmHg \big) 0.8 + 25 \; mmHg =85 \; mmHg
\rm Y_4 = { P_2 \over P_T } = { 80 \over 85 } = 0.941
İşlemi tekrarlarsak
\rm P_2 = P_2 ^o \chi _2 = (100 \; mmHg)(0.941) = 94.1 \; mmHg
\rm P_T = \big( P_2 ^o - P_1 ^o \big) \chi _2 + P_1 ^o = \big( 100 \; mmHg \; - \; 25 \; mmHg \big) 0.941 + 25 \; mmHg =95.575 \; mmHg
\rm Y_5 = { P_2 \over P_T } = { 94.1 \over 95.575 } = 0.985
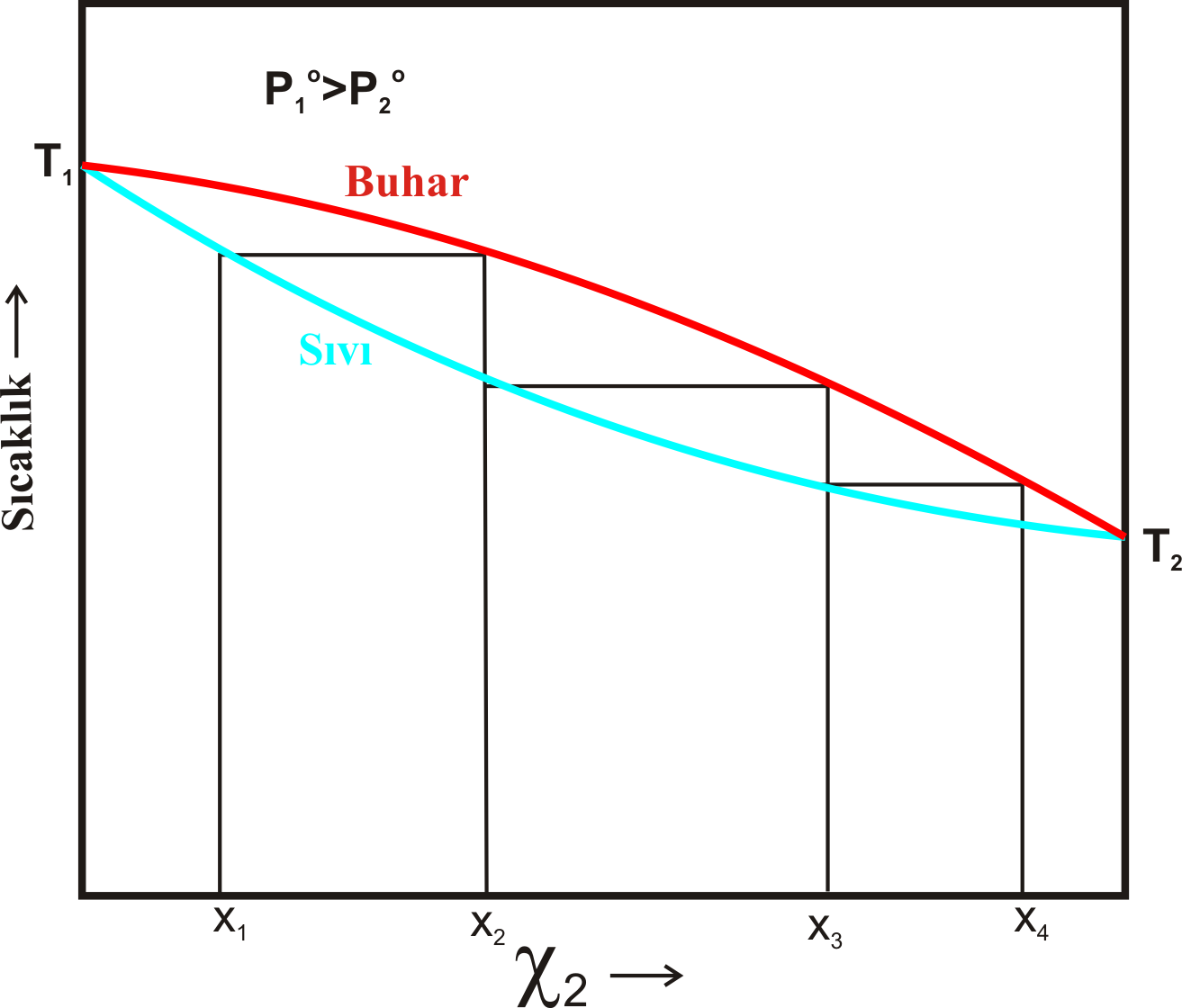
Şekil 2 : Sabit basınçta ikinci bileşenin mol kesrine karşı karışımın ve buharın bileşimi.
|
Görüldüğü gibi ikinci bileşenin saf haldeki buhar basıncı birinci bileşenin saf haldeki buhar basıncından büyükse
destilatta ikinci bileşen zenginleşecektir. Durum tersi ise destilatta birinci bileşen zenginleşecektir.
Yukarıdaki işlem sabit sıcaklık yerine sabit basınçta gerçekleştirilecek olursa grafik Şekil 2 deki gibi olacaktır.
Burada; aynı sıcaklıkta birinci bileşenin buhar basıncı ( \rm P_1) ikinci bileşenin buhar basıncı ( \rm P_2) den daha büyüktür.
Şekil 1-b ile Şekil 2 deki grafikler karşılaştırılırsa sıvı ve gaz fazların yerlerinin değiştiği görülür.
Ayrıca; \rm P_1 < P_2 olduğundan \rm X_1 yüksek olduğu bölgede kaynama sıcaklığının da yüksek olduğu görülür.
Elde edilen her bir destilatın kaynama noktası Şekil 1-b dekin de de olduğu gibi \rm X_2 açısından
daha zengin olduğundan daha düşük olur.
Şekil 3 de laboratuavar ölçeğinde için fraksiyonlu destilasyon düzeneği görülmektedir.
Bu düzenekte vakum uygulanarak daha düşük sıcaklıklarda destilasyon gerçekleştirilebilir.
Düşey şekilde bulunan soğutucunun karışımı fraksiyonlandırmak için kullanılır.
Kolondan yukarıya doğru çıkıldıkça saf haldeki buhar basıncı yüksek olan madde zenginleşir.
Termometredeki sıcaklık kontrol edilerek soğutucuya gecen buhar bileşimi tahmin edilebilir.
Fraksiyonlu Destilasyonda Tabaka Sayısı
Şekil 2 de görülen herbir buharlaşma - yoğunlaşma adımı, teorik bir plaka olarak kabul edilir.
Basit bir distilasyonda sadece bir tane teorik tabaka bulunmaktadır.
Fraksiyonlu distilasyonda pek çok tabaka bulunur ve bu tabakaların her birinde yeni bir distilasyon meydana gelir.
Teorik olarak bu plakaların sayısı , yoğunlaşma için mevcut olan yüzey alanına bağlıdır.
Bir fraksiyonlu destilasyon düzeneğinde ne kadar çok teorik plaka varsa, daha iyi bir ayırma olacak demektir.
Bu yüzden fraksiyonlu distilasyon, içerisinde kaynama noktaları birbirine yakın olan karışımları ayırmada kullanılan
çok etkili bir yöntemdir.
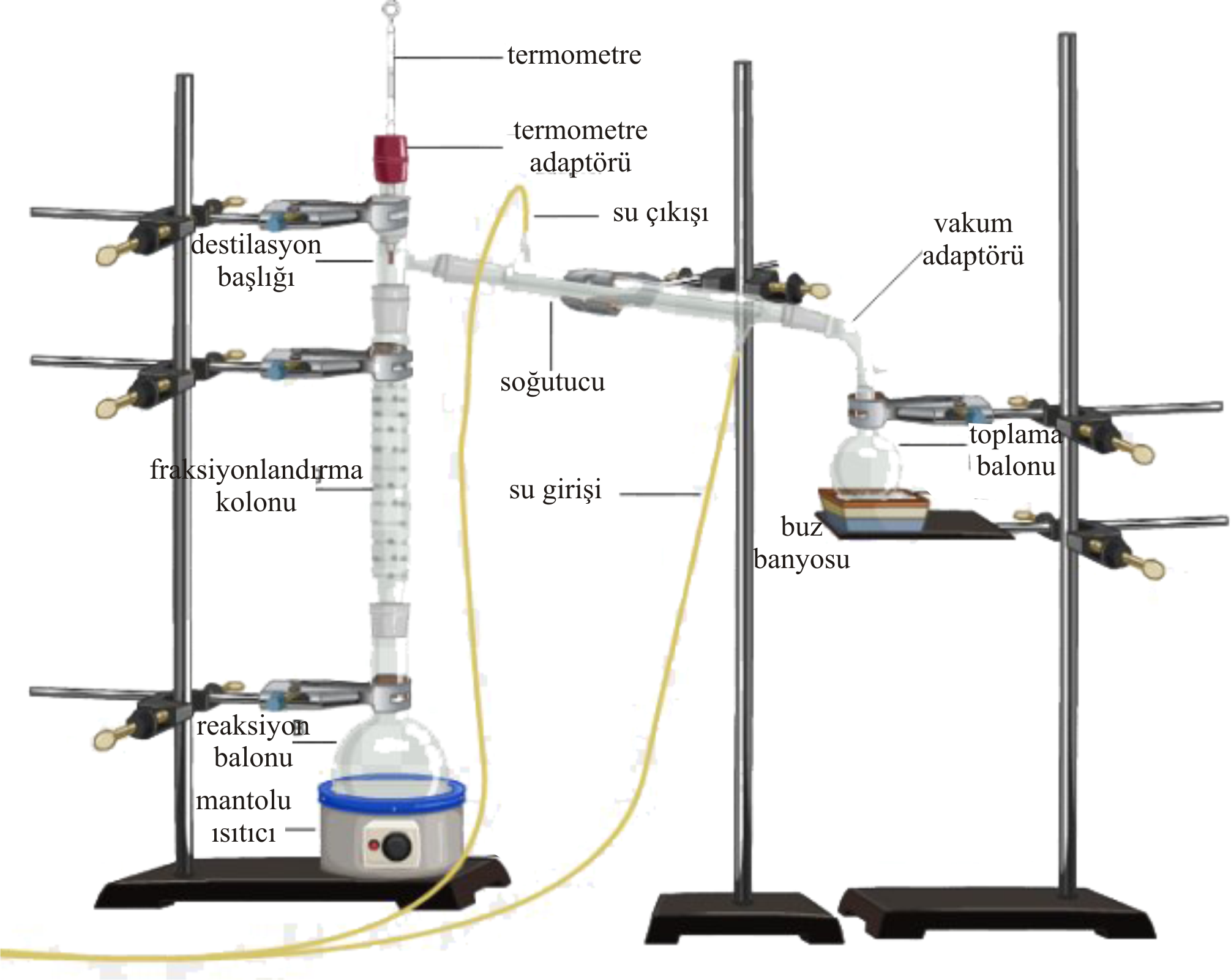
Şekil 3 :
Laboratuvar ölçeğinde fraksiyonlu destilasyon düzeneği.
|
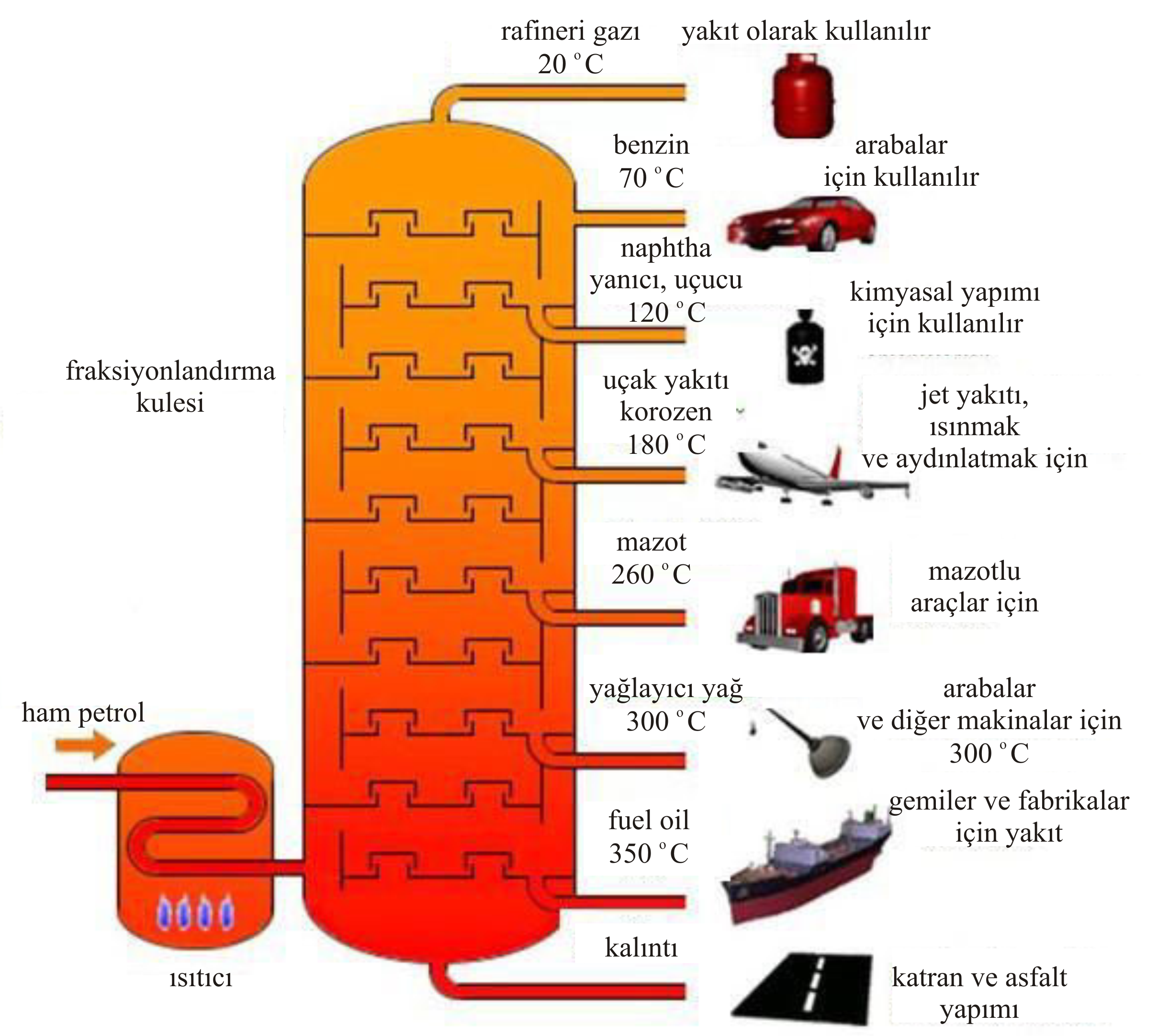
Şekil 4-a da ise petrol rafinerisi için kullanılan düzeneklerden birinin şematik çizimi görülmektedir.
Şekilde de görüldüğü gibi kulenin üst taraflarından buhar basıncı yüksek, kaynama noktası düşük maddeler
toplanırken, kulenin alt tarafları için tam tersi geçerlidir.
Şekil 4-b de ise endüstride kullanılan petrol rafinerisinin bir parçası görülmektedir.
Gerçek Sıvı Karışımlarında Buhar Basıncı
Moleküler etkileşmelerin bulunduğu gerçek sıvı karışımlarında bileşime bağlı olarak buhar basıncı değişimi
ideal davranış gösteren çözeltilerde olduğu gibi Raoult Kanununa uymaz.
Moleküler etkileşmeler nedeni ile herbir bileşenin kısmı basıncı beklenenden daha büyük veya daha küçük olabilir.
Bunun sonucu olarak da karışımın taplam buhar basıncı beklenen değerlerin bazen altında bazen üstünde yer alabilir.
Eğer karışımın buhar basıncı Raoult Kanunu ile beklenen değerden daha büyük ise, bu karışımlar için
Raoult Kanunundan pozitif sapma gösteren sıvılar olarak bahsedilir.
Eğer karışımın buhar basıncı Raoult Kanunu ile beklenen değerden daha küçük ise, bu karışımlar için
Raoult Kanunundan negatif sapma gösteren sıvılar olarak bahsedilir.
|

|
|
Şekil 4 : Sanayi ölçeğinde fraksiyonlu destilasyon (a) Şematik (b) Uygulamada.
|
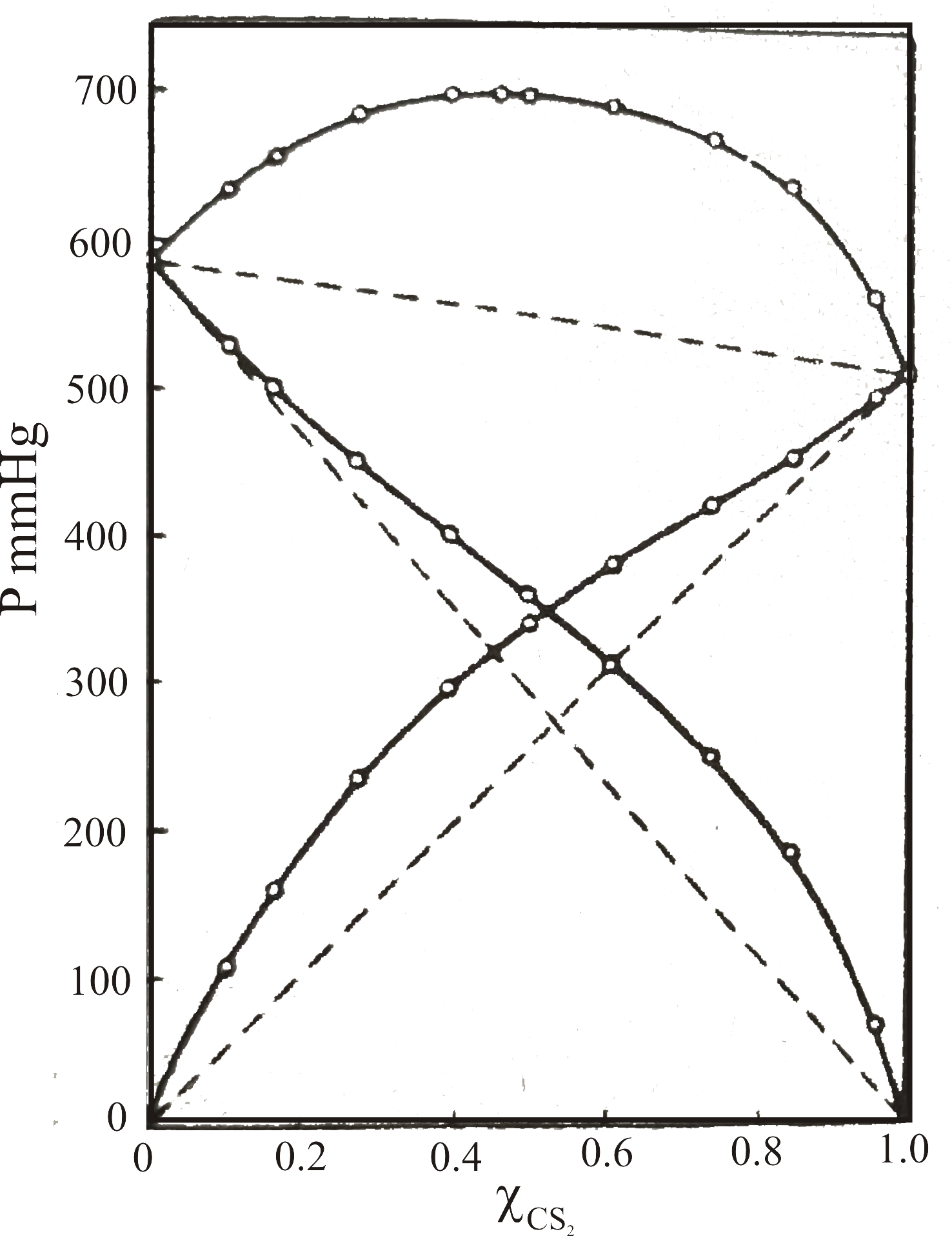
Bu tür davranış gösteren çözelti karışımlarına örnek olarak Şekil 5 deki grafikler örnek olarak verilebilir.
Şekil 5-a ' da 35.2 \rm ^oC de metil aldehit - karbonsülfürün sistemine ilişkin türlerin kısmı buhar basınçları ve sistemin
toplam buhar basıncı görülmektedir. Şekilden de açıkça görüldüğü gibi herbir türün kısmı basıncı Raoult kanunundan beklenen
değerden daha büyüktür. Sonuçta sistemin toplam buhar basıncı da beklenen değerden büyüktür.
Buhar basıncının artma nedeni, karışma nedeni ile moleküller arası kuvvetlerin azalmasından kaynaklanabilir.
|
2CO_HCCl3.png)
|
| (a) | (b) |
|
Şekil 5 : (a)
35.2 \rm ^oC de metil aldehit - karbonsülfür karışımında türlerin kısmı basınçları ve toplam buhar basıncı değişimi.
(b)
55.1 \rm ^oC de aseton - kloroform karışımında türlerin kısmı basınçları ve toplam buhar basıncı değişimi.
|
Şekil 5-b ' de ise 55.1 \rm ^oC de aseton - kloroform sistemine ilişkin türlerin kısmı buhar basınçları ve sistemin
toplam buhar basıncı görülmektedir. Şekilden de açıkça görüldüğü gibi herbir türün kısmı basıncı Raoult kanunundan beklenen
değerden daha küçüktür. Sonuçta sistemin toplam buhar basıncı da beklenen değerden küçüktür.
Buhar basıncındaki düşmenin nedeni moleküller arasındaki etkileşmeden kaynaklanabilir. Nitekim bu iki tür arasında moleküller arası hidrojen bağı oluşur.
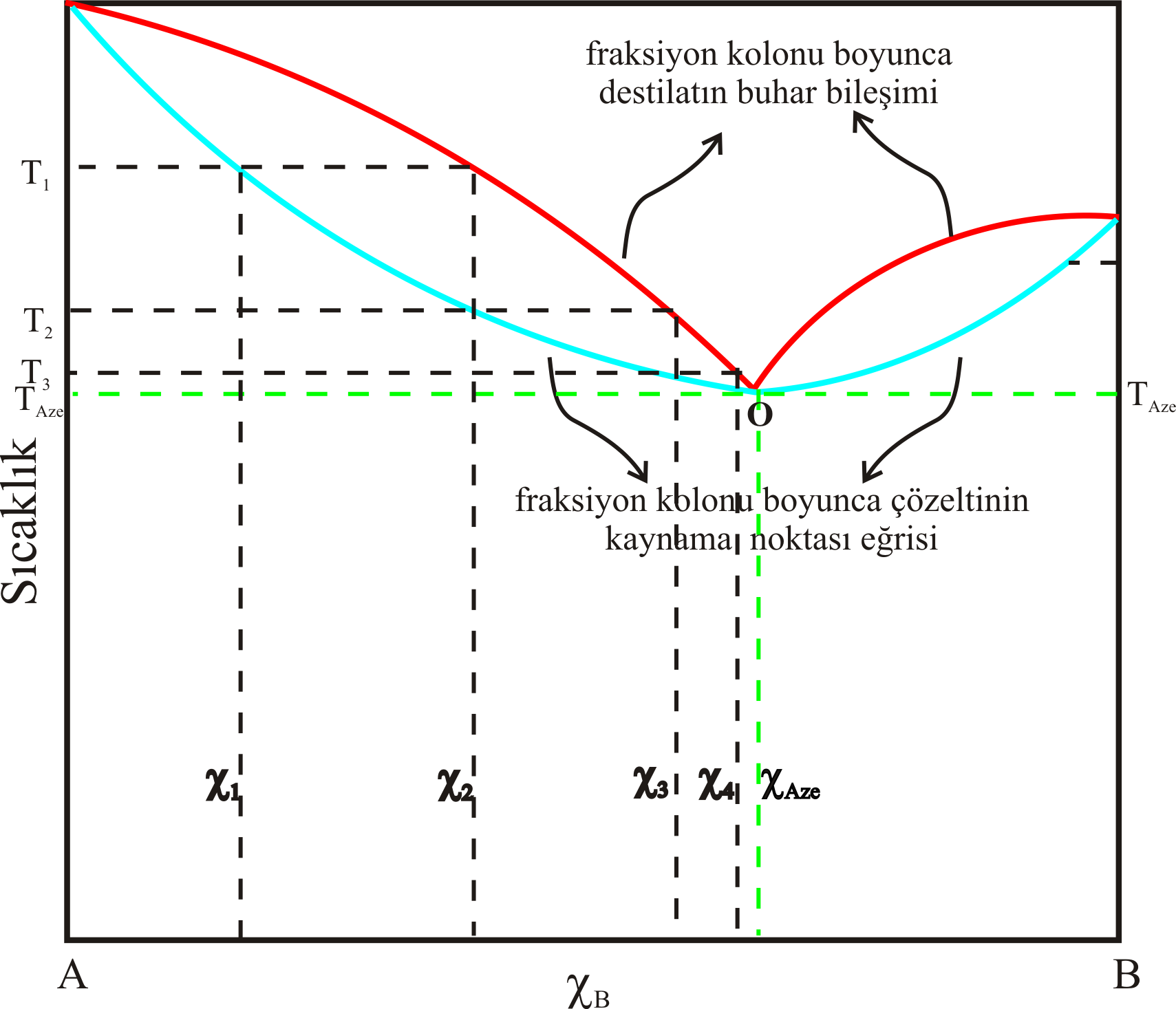
Şekil 5-a daki gibi sistemlerin sabit basınç altındaki bileşim sıcaklık eğrisi Şekil 6-a da görüldüğü gibidir.
Şekilden görüldüğü gibi \rm \chi _1 mol kesrindeki B içeren karışımın Şekil 3 deki gibi bir düzenek ile
destile edilirse, kolonun üst kısımlarındaki ilk tabakada \rm \chi _2 mol kesrinde sıvı oluşur.
Burada bahsettiğimiz tabaka kavramı hayali bir kavramdır.
Destilat bileşimine göre kolonun kaç tabakalı olduğu hesaplanabilir.
Bunu kolon boyunca yoğunlaşan kısımların ilk parçası olduğunu düşünebilirsiniz.
Birinci tabakadaki \rm \chi _2 bileşimindeki sıvının buhar bileşimi \rm \chi _3 tür.
Benzer mantıkla \rm \chi _4 bileşimindeki karışıma ve sonunda \rm \chi _{Azo} bileşimine sahip
\rm T_{Azo} sıcaklığıdaki buhar soğutucuda yoğunlaşır.
Sonuçta sistemdeki çözelti kaynarken Şekil 3 deki termometrenin sürekli olarak olarak \rm T_{Azo}
sıcaklığını gösterdiğini ve destile edilen karışımdaki B nin mol kesrinin de \rm \chi _{Azo} olduğunu görürüz.
Bu tür sistemler Raoult Kanunun'dan pozitif sapma gösteren, kaynama sırasında bileşimi değişmeyen ( \rm \chi _{Azo} ) ve sabit kaynama noktalı ( \rm T _{Azo} )
karışımlara örnektir.
Bu şekilde bileşimi değişmeden kaynayan, bileşimini koruyan ve sabit kaynama noktalı karışımlara azeotrop denir.
|
2CO_HCCl3_SP.png)
|
| (a) | (b) |
|
Şekil 6 : (a)
Sabit basınçta minimum kaynama noktası gösteren karışım
(b)
Sabit basınçta maksimum kaynama noktası gösteren karışım
|
Şekil 5-b daki gibi sistemlerin sabit basınç altındaki bileşim sıcaklık eğrisi Şekil 6-b da görüldüğü gibidir.
Şekilden görüldüğü gibi \rm \chi _1 mol kesrindeki B içeren karışımın Şekil 3 deki gibi bir düzenek ile
destile edilirse, karışım \rm T_1 sıcaklığında kaynamaya başlar. Buhar bileşimindeki B nin mol kesri \rm \chi _1
e göre daha küçüktür. Bu kaynama sırasında Şekil 3 deki termometreden \rm T_1 değeri okunur.
Karışım böylece B açısından zenginleşerek \rm \chi _2 doğru zenginleşir termometreden okunan değerde \rm T_1 den
\rm T_2 ye doğru yükselir.
Karışım kaynama devam ettirilirse buhar fazındaki mol kesri karışım içine göre düşük olan B, karışım içinde mol kesri \rm \chi _2 den
\rm \chi _3 doğru artarken karışımın sıcaklığı da \rm T_2 den \rm T_3 doğru artar.
Karışım kaynamaya devam ettirilirse, karışım içindeki B nin mol kesri \rm \chi _3 den \rm \chi _{Azo}
ya kadar yükselirken sıcaklıkta \rm T_3 den \rm T_{Azo} ya doğru yükselir.
Bu noktadan sonra karışım kaynamaya devam ettirilse de karışımın bileşimi \rm \chi _{Azo} de sabit kalırken
sıcaklığı da \rm T _{Azo} da sabit kalır.
Bu tür sistemler Raoult Kanunun'dan negatif sapma gösteren, kaynama sırasında bileşimi değişmeyen ( \rm \chi _{Azo} ) ve sabit kaynama noktalı ( \rm T _{Azo} )
karışımlara örnektir.
Bu şekilde bileşimi değişmeden kaynayan, bileşimini koruyan ve sabit kaynama noktalı karışımlara azeotrop demiştik.
Tablo 1 de minimum ve maksimum kaynama noktalı karışımlara örnekler verilmiştir.
Maksimum kaynama noktalı karışımlardan Su-HCl örneği ele alınırsa, herhangi bir Su-HCl örneği kaynatılırsa,
kaynamanın 108.5 \rm ^oC de sabit kaldığı ve çözelti bileşiminde ağırlıkça %20.24 HCl içeridiği görülür. Böylece bilinen konsantrasyonda hidroklorik asit çözeltisi bu şekilde elde edilebilir.
Tablo 1 : Saf maddelerin molar termodinamik özelikleri.
| Tür |
A (Kay.Nok. \rm ^oC) |
B (Kay.Nok. \rm ^oC) |
Kaynama Nok. \rm ^oC |
Azeotropik Karışımda
Ağırlıkça %B |
Minimum
Kaynama
Kaynamalı |
su (100) |
etil alkol (78.37) |
78.15 |
95.57 |
| su (100) |
n-propil alkol (98) |
87.72 |
71.70 |
| etil alkol (78.37) |
benzen (80.1) |
68.24 |
67.63 |
| asetik asit (118) |
benzen (80.1) |
80.05 |
98 |
| karbon sülfür (46.3) |
etil asetat (77.1) |
46.1 |
3 |
| pridin (115) |
su (100) |
92.6 |
43 |
Maksimum
Kaynama
Kaynamalı |
su (100) |
nitrik asit (83) |
120.5 |
68 |
| su (100) |
HCl ( ) |
108.5 |
20.24 |
| su (100) |
HBr ( ) |
126.0 |
47.5 |
| su (100) |
HI ( ) |
127 |
57 |
| su (100) |
HF ( ) |
120.0 |
37 |
| su (100) |
formik asit (100.8) |
107.1 |
77 |
| kloroform (61.2) |
aseton (56) |
64.7 |
20 |
| pridin (115) |
formik asit (109.8) |
149.0 |
18 |
|