İdeal Çözeltiler İdeal gazları tanımlarken molekülleri arasında herhangi bir fiziksel veya kimyasal etkileşmenin olmadığı PV=nRT genel gaz denklemine göre hareket ettiklerini söylemiş ve gazlar bu davranıştan saptıklarında gerçek gaz davranışı gösterdiğini söylemiştik. Ayrıca tüm gazların yüksek basınç ve düşük sıcaklık değerlerine doğru gidildikçe ideallikten saparak gerçek gaz davranışı gösterdiklerini örneklerle açıklamıştık. İdeal çözelti de çözücü ve çözünen molekülleri arasında herhangi bir fiziksel veya kimyasal etkileşmenin olmadığı çözelti olarak tanımlanır. İdeal çözeltilerde teorik olarak tanımlanır ve gerçekte tam olarak ideal davranış gösteren çözeltiler yoktur. Ancak ideal çözelti davranışına yakın davranış gösteren çözeltiler söz konusudur. Daha önce karışım içindeki bir madde için Gibbs serbest enerjisi ile aktifliği arasında \rm G = {\overline G}^o + n RT ln a eşitliğini çıkartmıştık. Buna göre; çözelti içindeki maddenin serbest enerji büyüklüğü ile aktivitesi arasında doğru orantılı bir ilişki söz konusuydu. Moleküler etkileşmeler nedeni ile maddenin aktifliği, konsantrasyonu artışı ile artmış olsa da doğru orantılı değildi. Aktiflik katsayısı denilen bir düzeltme faktörü ile düzeltilmişti ( a=fC ). aktiflik katsayısı aslında moleküller arası etkileşmelerin artması ile arttan bir sayıdır. İdeal çözeltilerde moleküller arası etkileşmeler olmayacağından aktiflik katsayısı değeri de 1 olmalıdır. Böylece ideal davranış gösteren çözeltilerdeki bir maddenin aktifliği konsantrasyonuna eşit olmalıdır (a = C). İdeal çözelti; bileşenlerinin herbirinin aktifliğinin tüm sıcaklık, basınç ve konsantrasyon değerlerinde çözelti içindeki mol kesrine eşit olan çözeltilerdir. Bu tanıma göre daha önce \rm \Delta G_{karışım} = n_1 RT ln a_1 + n_2 RT ln a_2 şeklinde yazdığımız eşitliği ideal davranış gösteren çözeltiler için, mol kesirlerine bağlı olarak \rm \Delta G_{karışım} = n_1 RT ln \chi _1 + n_2 RT ln \chi _2 şeklinde yazabiliriz. Bu ifadeden görüldüğü gibi eşitliğin sağ tarafı basıçtan bağımsızdır. Bu nedenle, ideal bir çözelti için; \rm \Big( { \partial \Delta G_{karışım} \over \partial P } \Big) _T = \Delta V = 0 olmalıdır. Buradan da görüldüğü gibi, ideal davranış gösteren bir çözeltide karışım öncesindeki hacim ne kadar ise, çözelti oluştuğunda da hacim aynı miktarda olmalıdır. Sabit basınçta \rm \Delta G_{karışım} \over T oranının sıcaklığa göre türevi alınırsa; \rm \Big[ { \partial { \Delta G_{karışım} \over T } \over \partial T}\Big] _P = -{ \Delta H_{karışım} \over T^2} = { \partial (n_1 R ln \chi _1) \over \partial T} + { \partial (n_2 R ln \chi _2) \over \partial T} = 0 olmalıdır. Bu eşitliğin doğru olması ancak \rm \Delta H_{karışım} = 0 olması ile mümkündür. Bir başka deyişle; ideal bir çözelti oluşumu endotermik veya ekzotermik olmamalıdır. Entalpi değişimi söz konusu olmayacağından; çözeltinin serbest enerji değişimi ; Şekil 1 : iki bileşenli ideal bir sistemde 298 K de 1 mol çözücü karışımı için bileşenlerden birinin mol kesrine karşı \rm \Delta G_{karışım}, \; \Delta H_{karışım} \; ve \; T \Delta S_{karışım} değerlerinin değişimi. \rm \Delta G_{karışım} = \Delta H_{karışım} - T \Delta S_{karışım} \rm \Delta G_{karışım} = - T \Delta S_{karışım} \rm \Delta G_{karışım} = n_1 RT ln \chi _1 + n_2 RT ln \chi _2 olmalıdır. Bu son eşitlikten de görüldüğü gibi \rm \Delta S_{karışım} çözeltideki bileşenlerin miktarı ve konsantrasyonlarına bağımlı olarak değişir. Son eşitlik toplam 1 mol karışım için; \rm \Delta G_{karışım} = \chi _1 RT ln \chi _1 + \chi _2 RT ln \chi _2 \rm \Delta G_{karışım} = RT \big( \chi _1 ln \chi _1 + \chi _2 ln \chi _2) olarak yazılabilir. 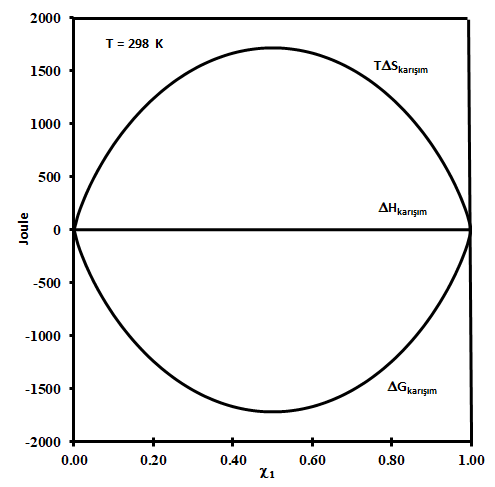1 mol çözelti karışımı için entropi değişimi ise; \rm \Delta S_{karışım} = -R \big( \chi _1 ln \chi _1 + \chi _2 ln \chi _2) Şekil 1 de ideal davranış gösteren ikili çözelti karışımının 1 molü için 298 K deki \rm \Delta G_{karışım}, \; \Delta H_{karışım} \; ve \; T \Delta S_{karışım} değerlerinin değişimi görülmektedir. (a) (b) Şekil 2 : Karbontetraklorür - Siklohekzan sisteminde karbontetraklorür mol kesrine bağlı olarak (a) \rm 25 \; ^oC,\; 30 \; ^oC,\; 70 \; ^oC de molar hacim yüzdesindeki değişimler (b) \rm 25 \; ^oC,\; 70 \; ^oC de karışımlar için entalpi, iç enerji, Gibbs serbest enerjisi ve Helmholtz serbest enerjilerindeki değişim. 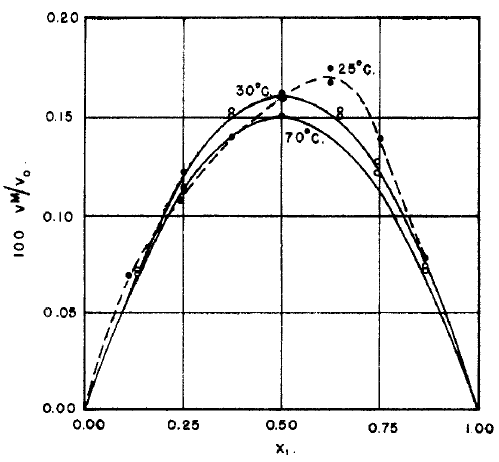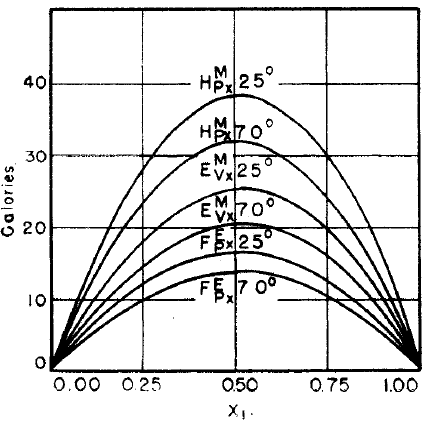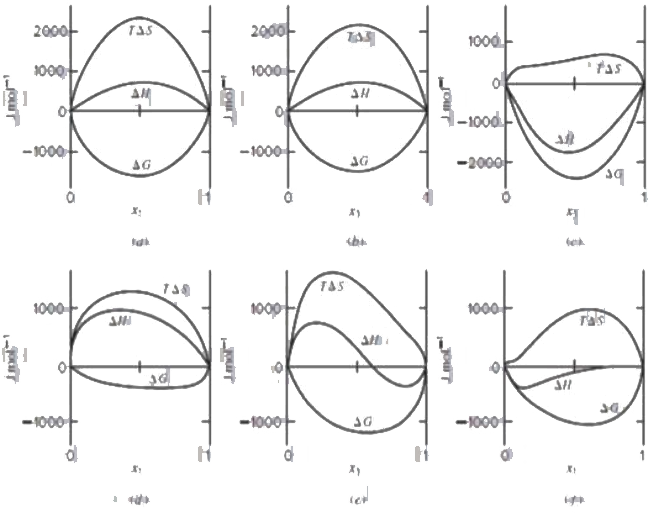Şekil 2 de nispeten ideal davranış gösteren karbontetraklorür - siklohekzan sistemi için hacim değişim ve entalpi değişimi görülmektedir. Şekil 3 de ise ideallikten oldukça sapan 6 farklı karışım için termodinamik paramatrelerdeki değişiklikler görülmektedir. Şekil 2 ve 3 deki sayısal değerler birbiri ile karşılaştırıldığında, Şekil 2 deki karışımın entalpi değişimi maksimum 40 kalori seviyesindeyken, Şekil 3 deki karışımlarda bu değerin \rm \pm 500-2000 kalori arasında olduğu görülmektedir. Şekil 3 : \rm 50 \; ^oC,\; de (a) kloroform(1) - n-heptan(2) (b) aseton(1) - metanol(2) (c) aseton(1) - kloroform(2) (d) etanol(1) - n-heptan(2) (e) etanol(1) - kloroform(2) (f) etanol(1) - su(2) sistemleri için \rm \Delta G_{karışım}, \; \Delta H_{karışım}, \; T \Delta S_{karışım} değişimi.