Birbiri İle Kısmen Karışan Sıvılar Birbiri ile kısmen karışan sıvılar, birbiri içinde az miktarda çözünebilen sıvılardır. Örneğin A sıvısı içerisinde B sıvının çözünürlüğü düşükse, A sıvısına çok az miktarda B eklendiğinde A içinde çözünür. A çözücüsü B sıvısına doyduğunda, daha fazla B eklendiğinde ikinci bir faz oluşturur. Tersi durumda, yani B sıvısına çok az miktarda A sıvısı eklendiğinde, A sıvısı B sıvısında çözünür. B sıvısına yeterince A eklendiğinde B sıvısı da A sıvısına doyar, daha fazla A eklenirse A sıvısı bir faz olarak ayrılır. Sonuç olarak kısmen B sıvısı A sıvısı içerisinde kısmen çözünürken, A sıvısı da B içerisinde kısmen çözünür. Bu tür karışımların birbiri içinde karışma miktarları sıcaklığa bağlı olarak değişir. 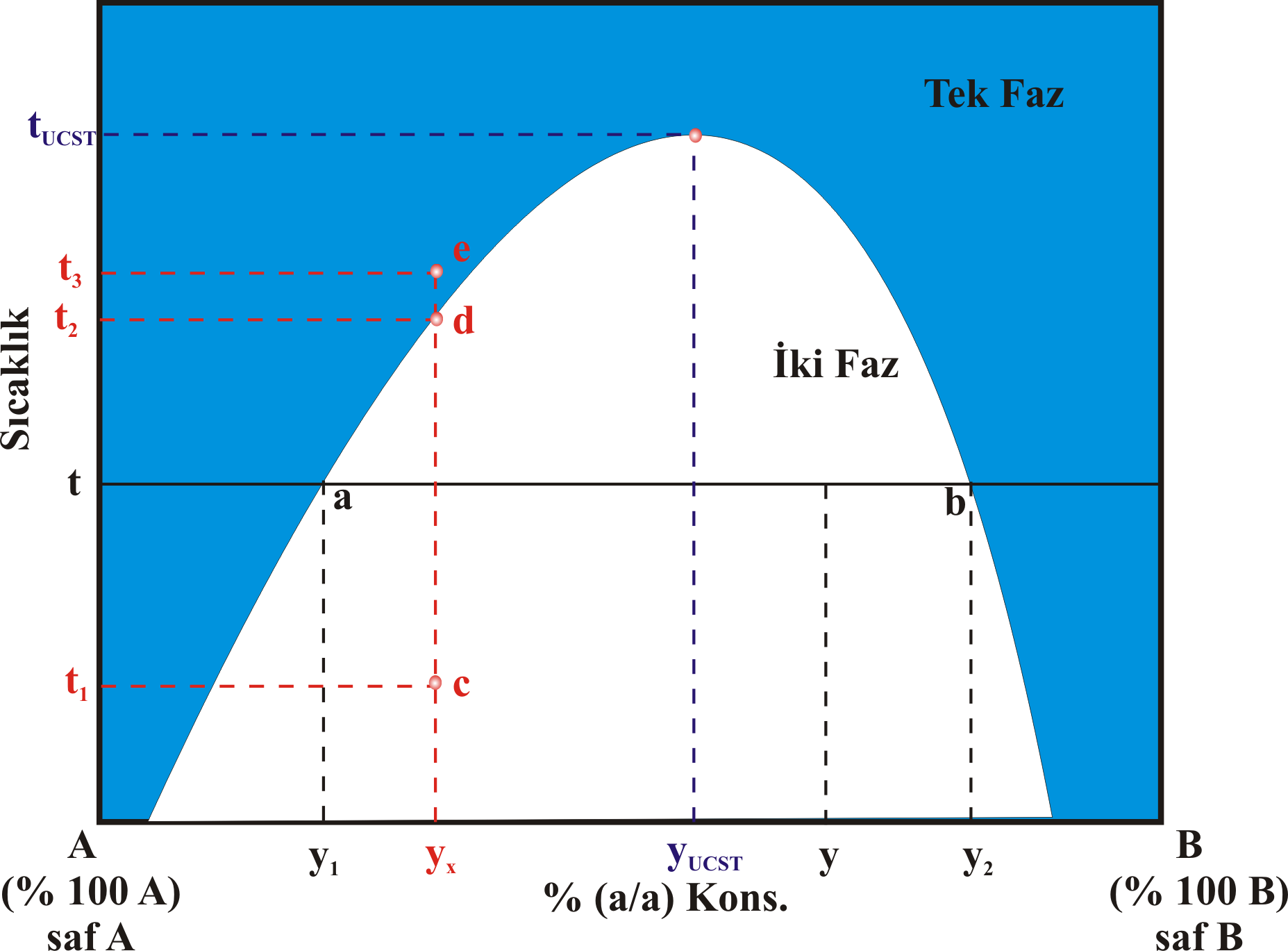Bu karışımları; Üst kritik çözünme sıcaklığına sahip karışımlar (UCST) Alt kritik çözünme sıcaklığına sahip karışımlar (LCST) Alt ve üst kritik çözünme sıcaklığına sahip karışımlar Alt ve üst kritik çözünme sıcaklığına sahip olmayan karışımlar olarak gruplandırabiliriz. (1). Üst Kritik Çözünme Sıcaklığına Sahip Karışımlar Bu karışımların bileşim-sıcaklık grafiği Şekil 1 de görüldüğü gibidir. Bazı bileşim ve sıcaklıklarda sistem tek fazlı iken, bazı bileşim ve sıcaklıklarda ise 2 fazlıdır. Örneğin \rm y_x \; ve \; t_1 sıcaklığında sistem c noktasında olup iki fazlıdır. \rm y_x \; ve \; t_1 sıcaklığındaki karışımın sıcaklığı arttırılırsa, sıcaklık \rm t_2 değerine ulaştığında kritik bir noktaya ulaşılır. Sıcaklık biraz daha arttırılırsa karışım tek fazlı hale gelecektir. \rm t_3 sıcaklıklığına ulaşan karışımda tek fazlıdır. bu sıcaklığın üstündeki sıcaklıklarda sistem tek fazlıdır. Şekil 1 : Üst kritik çözünme sıcaklığına sahip A-B karışımın bileşim-sıcaklık grafiği. \rm y_x \; ve \; t_3 sıcaklığında e noktasında bulunan karışım yavaşça soğutulursa, tekrar \rm t_2 sıcaklığında kritik nokta olan d noktasına ulaşılır. Bu noktanın hemen altında karışım yeniden iki fazlı hale gelecektir. Ancak bu geçiş sırasında iki faz birbirindan aniden ayrılmaz. Bu örnekte B daha az olduğudan A içinde dağılacaktır. Bu dağılma öncesinde homojen ve berrak olan tek fazlı karışım, B nin A içinde gözle görülmez kürecikler şeklinde ayrılırken, karışımın bulanıklaştığı görülür. Bu bulanıklaşmanın görüldüğü noktaya bulutlanma noktası adı verilir. Bulutlanmanın oluşup kaybolduğu nokta ne kadar iyi tespit edilirse, \rm y_x bileşimindeki karışım için kritik nokta olan \rm t_2 sıcaklığı kadar hassas olarak belirlenebilir. t sıcaklığıda bulunan A içine sıcaklığı değişmeden çok az miktarda B eklendiğinde, A içerisinde B çözünür ve sistem tek fazlı olur. Karışıma t sıcaklığı değişmeksizin B eklenmeye devam edildiğinde, karışım içindeki B miktarı \rm y_1 değerine, a noktasına ulaşır. Bu nokta A nın B doyduğu noktadır. Bundan sonra eklenen B ikinci bir faz oluşturacaktır. Benzer şeyler B fazına A eklenmesi içinde söylenebilir. t sıcaklığındaki B ye sıcaklığı değişmeksizin çok az miktarda A eklenirse A, B fazı içerisinde çözünür. t sıcaklığıdaki bu karışıma daha fazla A eklenecek olursa, B nin konsantrasyonu \rm y_2 değerine kadar geriler. Bu noktada; B, A ya doymuştur. Daha fazla A eklenecek olursa; A, B içinde dağılır. Sonuç olarak; A ve B sıvıları iki fazlı B nin karışım içindeki konsantrasyonunun y olduğu bir sistem oluşturduklarında; A fazında çözünmüş olarak B bulunur ve A fazındaki B nin konsantrasyonu \rm y_2 dir. Diğer taraftan B fazının içinde de A çözünmüş olarak bulunur ve bu nedenle B fazındaki B konsantrasyonu \rm y_2 dir. Bir Arada Bulunan Fazların Miktarı : Kaldıraç Kuralı Şekil 1 de görülen t sıcaklığıda ve y bileşimindeki sistemdeki herbir fazın kütlesinin ne kadar olduğunu hesaplayalım. A fazında B çözündüğü için; A fazının kütlesini \rm m_{A(B)} olarak, B fazında A çözündüğü için; B fazının kütlesini \rm m_{B(A)} olarak gösterirsek sistemin toplam kütlesi \rm m_T ; \rm m_T = m_{A(B)} + m_{B(A)} olacaktır. B bileşeninin \rm m_T ağırlığındaki toplam kütlesi; \rm y(m_T), A fazındaki B nin kütlesi \rm y_1 m_{A(B)}, B fazındaki B nin kütlesi; \rm y_2 m_{B(A)} olacağından; \rm y(m_T) = y_1 m_{A(B)} + y_2 m_{B(A)} \rm y \big( m_{A(B)} + m_{B(A)} \big) = y_1 m_{A(B)} + y_2 m_{B(A)} yazılabileceğinden \rm { m_{A(B)} \over m_{B(A)} } = { y_2 - y \over y - y_1} elde edilebilir. Bu eşitlik dengede bulunan A ve B fazlarının oranını bulmak için kullanılır. Bu kural kaldıraç kuralı olarak adlandırılır. (a) (b) Şekil 2 : Üst kritik çözünme sıcaklığına sahip olan (a) fenol - su (b) anilin - su sistemlerinin bileşim - sıcaklık grafiği. 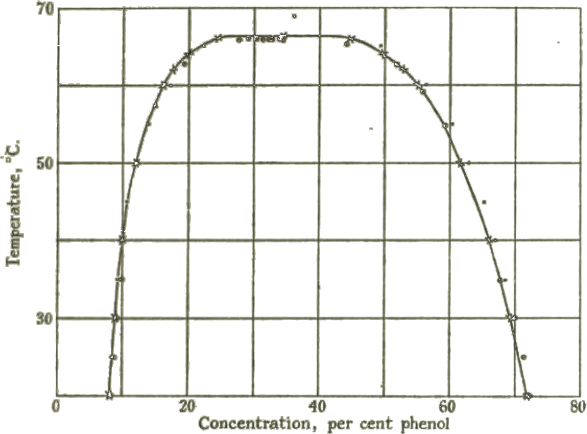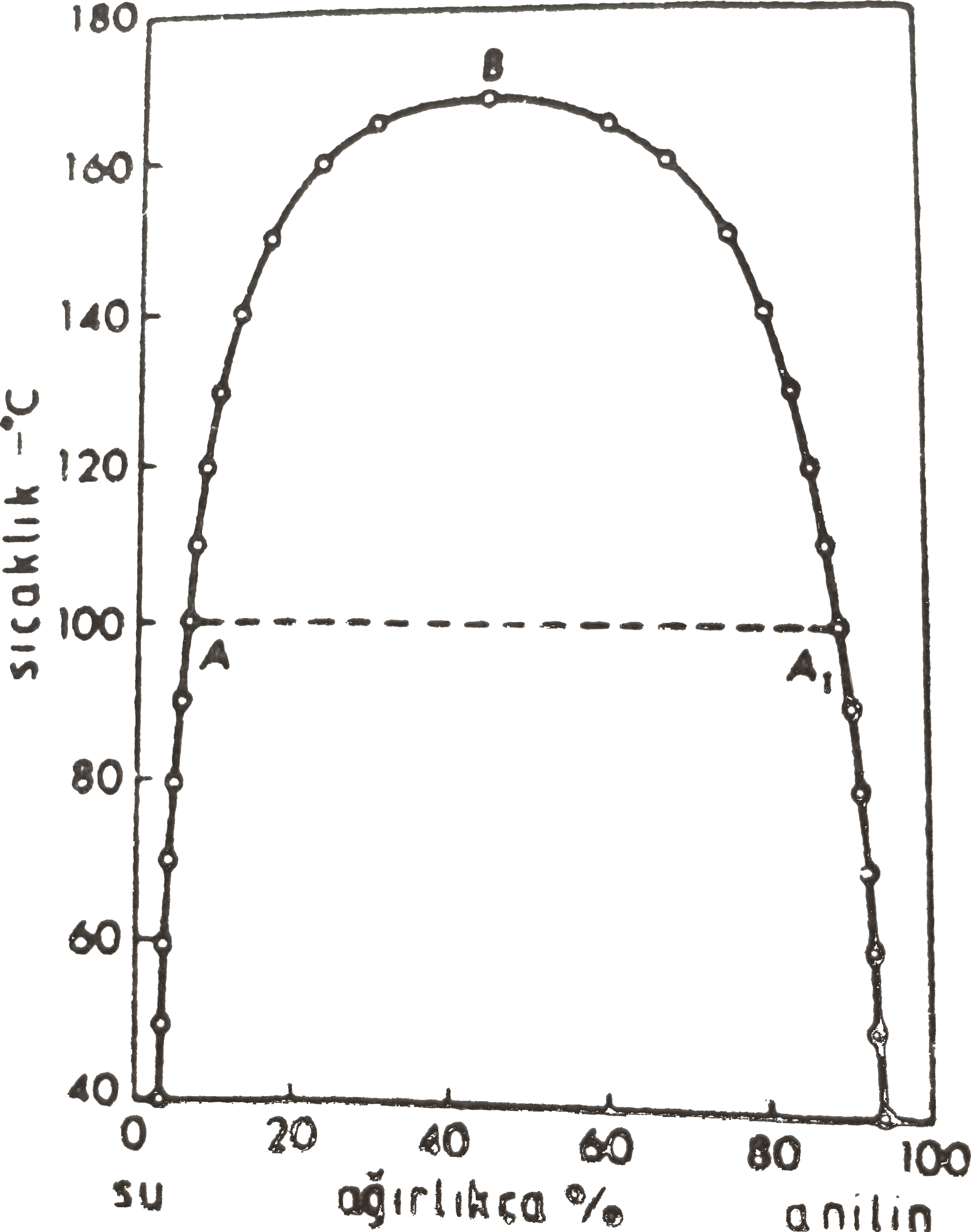Şekil 2-a da üst kritik çözünme sıcaklığına sahip fenol- su sistemi, Şekil 2-b de ise anilin-su sistemlerinin bileşim-sıcaklık grafikleri görülmektedir. 40 \rm ^oC deki ağırlıkça %40 fenol içeren 150 g. fenol-su sistemindeki; fenol kütlesini ve su kütlesini fenol fazının ve su fazının kütlesini su fazındaki fenol kütlesini fenol fazındaki su kütlesini hesaplayınız. (a). fenol kütlesi ve su kütlesi: \rm m_{fenol}=(150 \; g \; karışım) \Big( { 40 \; g \; fenol \over 100 \; g \; karışım } \Big) = 60 \; g \; fenol \rm m_{su}=(150 \; g \; karışım) \Big( { 60 \; g \;su \over 100 \; g \; karışım } \Big) = 90 \; g \; su (b). fenol fazının ve su fazının kütlesi: Kaldıraç kuralı kullanılarak fazların oranları hesaplanabilir. Bunun için Şekil 2-a deki grafikten yaklaşık olarak \rm y_1=10 , \rm y_2=67 olarak bulunabilir. \rm { m_{su(fenol)} \over m_{fenol(su)} } = { y_2 - y \over y - y_1} \rm { m_{su(fenol)} \over m_T - m_{su(fenol)} } = { y_2 - y \over y - y_1} \rm { m_{su(fenol)} \over 150 \; g - m_{su(fenol)} } = { 67 - 40 \over 40 - 10} = 0.9 \rm m_{su(fenol)} = 71.1 \; g. \rm m_{fenol(su)} = m_T - m_{su(fenol)} \rm m_{fenol(su)} = 150 \; g. - 71.1 \; g. = 78.9 \; g. (c). su fazındaki fenol kütlesi Su fazı %10 fenol içerdiğinden (grafikten \rm y_1 değeri) ve 71.1 g. su fazı bulunduğundan, su fazındaki fenol kütlesi \rm m_{fenol} (su \; fazında) = 71.1 \;g. \; su \; fazı \Big( { 10 \; g. fenol \over 100 \; g. A \; fazı } \Big) = 7.11 \; g. \; fenol \; içerir. (d). fenol fazındaki su kütlesi Fenol fazı %67 fenol içerdiğinden (grafikten \rm y_2 değeri) % (100-67) = % 33 g su içerir. ve 78.9 g. fenol fazı bulunduğundan, fenol fazındaki su kütlesi \rm m_{su} (fenol \; fazında) = 78.9 \;g. \; fenol \; fazı \Big( { 33 \; g. fenol \over 100 \; g. A \; fazı } \Big) = 26.037 \; g. \; su \; içerir.   Benzer bir soruyu farklı değerleri için çözümlemek için tıklayın. (2). Alt Kritik Çözünme Sıcaklığına Sahip Karışımlar Alt kritik çözünme sıcaklığına sahip sistemlere örnek olarak Şekil 3-a daki trietilen amin - su sistemi verilebilir. Bu sistemde 18.5 \rm ^oC altındaki sıcaklıklarda iki tür birbiri içinde her oranda çözünebilir. Bu nedenle bu sistem için 18.5 \rm ^oC alt kritik çözünme sıcaklığıdır (LCST). Bu sıcaklığın üzerindeki sıcaklıklarda fazların bir biri içinde çözünme miktarı azalmaktadır. (a) (b) Şekil 3 : (a) trietilamin - su karışımları için bileşim sıcaklık değişim eğrisi. (b) nikotin - su karışımları için bileşim sıcaklık değişim eğrisi (3). Alt Kritik Çözünme Sıcaklığı (LCST)ve Üst Kritik Çözünme Sıcaklığına (UCST) Sahip Karışımlar Nikotin - su karışımları bu sistemlere örnek olarak verilebilir. Şekil 3-b de; nikotin - su için, bileşim -sıcaklık grafiği görülmektedir. Nikotin - su sistemi için üst kritik çözünme sıcaklığı 208 \rm ^oC ve alt kritik çözünme sıcaklığı 60.8 \rm ^oC dir. Nikotin - su sistemleri ile yapılan deneylerde dış basıncın arttırılması ile kritik değerlerin birbirine yaklaştıkları görülmüştür. (3). Kritik Çözünme Sıcaklığına Sahip Olmayan Karışımlar Bu sınıf altında örnek olarak dietil eter - su karışımları verilebilir. Birbiri içinde kısmen çözünselerde, alt ve üst kritik sıcaklık değerlerine sahip değildir. 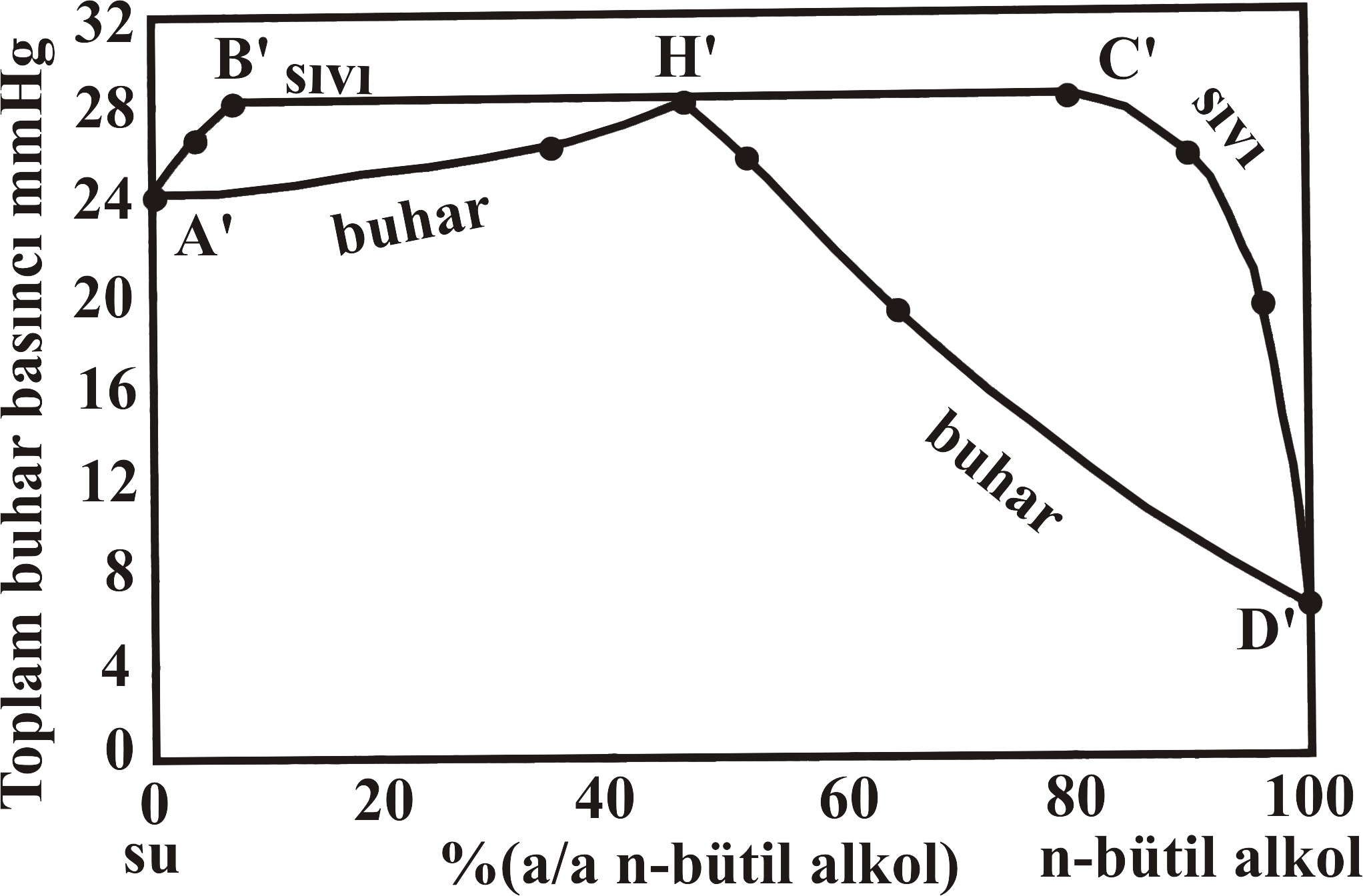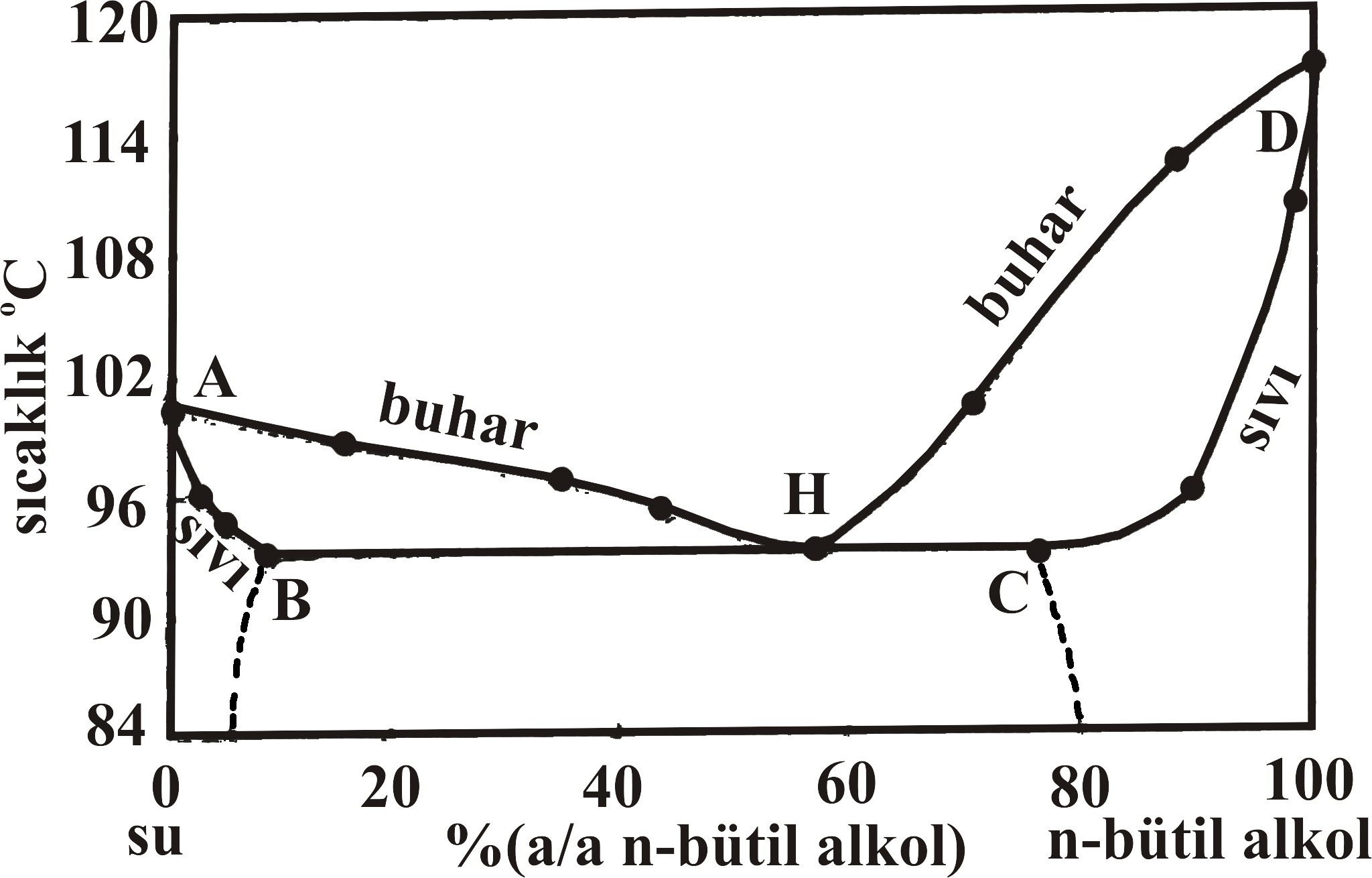Birbiri İle Kısmen Karışabilen Sıvıların Destilasyonu ve Buhar Basınçları Şekil 4 de biribiri içerisinde kısmen çözünen n-bütil alkol - su karışımı için yüzde bileşime karşın buhar basıncı değişimi, ve sıcaklık değişim grafikleri verilmiştir. Şekil 4-a da D' noktası 25 \rm ^oC saf n-bütil alkolün buhar basıncını gösterirken, Şekil 4-b de D noktası 760 mmHg da saf n-bütil alkolün kaynama noktasını göstermektedir. Saf n-bütil alkole su eklendikçe buhar basıncı artarak C' noktasına doğru yaklaşırken, kaynama noktası da düşerek C noktasına yaklaşmaktadır. Bu noktadan sonra eklenen su ile buhar basıncı C' noktasından B' noktasına kadar değişim göstermezken, Kaynama noktası da C noktasından B noktasına kadar sabit kalmaktadır. (a) (b) (c) Şekil 4 : (a) n-bütil alkol - su sistemi için 25 \rm ^oC de yüzde bileşim - buhar basıncı değişimi. (b) n-bütil alkol - su sistemi için 760 mmHg de yüzde bileşim - sıcaklık değişimi. (c) n-bütil alkol - su sistemi için yüzde bileşim - sıcaklık faz diyagramı. B' noktası ve C' noktası arasında buhar basıncı sabit olup H değerine eşittir. Şekil 4-b deki B ve C noktalarındaki kesikli çizgiler iki sıvı bileşenin karşılıklı çözünürlüklerinin sıcaklık ile değişimini göstermektedir.