Yanıt : Atmosfer basıncı;Pdış= 765 mmHg ve sağ koldaki civa yüksekliği 12 cm fazla olduğundan Hava örneğinin basıncı;
Yanıt : Gazın başlangıçtaki Hacmi ve basıncı ; V1 = 3.00 L, P1 = 12.00 atm. dir. Sıcaklık değişmediğinden
PV değeri sabit olacağından;
PixVi=PsxVs
Vs=PixVi/Ps = L.
Vs=(12 atm.)x(3.00 L)/(0.032 atm.) = 1125 L.
Yanıt : Atmosfer basıncı;Pdış= 765 mmHg ve sağ koldaki civa yüksekliği 12 cm fazla olduğundan Hava örneğinin basıncı;
PHava = 765 mmHg + 120 mmHg = 885 mmHg dır.
civa seviyeleri arasındaki fark 15 cm çıkarsa hava örneğinin gaz basıncı;
PHava = 765 mmHg + 150 mmHg = 915 mmHg
değerine ulaşır.
Yanıt :Gazın 30 oC deki hacminin V30 olduğunu düşünelim. Sıcaklığın 5 oC değişmesiyle hacim V35-V30= 12 cm3 değişmiştir. Buna göre;
| {V_i \over T_i } = {V_s \over T_s } |
| {V_{30} \over (273.16 + 30) K } = {(V_{30} + 12) cm^3 \over (273.16 + 35 ) K } |
| V_{30} = 727.584 cm^3 |
Yanıt : Pi= 1 atm., Vi= 1.00 L, Ti= 273.16+ 15 K dir. Daha sonra Ps= 1.6x10-11 atm., Ts= 1580 K değerine değişmiştir. Bileşik gaz yasasına göre sonuç kolayca bulunabilir.
| V_s = ({P_i V_i \over T_i })({T_s \over P_s}) |
| V_s = ({(1.0\, atm.) (1.0 \, L.) \over 288.16 \, K })({1580 \, K \over 1.6\times 10^{-11} \, atm.}) |
| V_s = 3.43 \times 10^{11} \, L. |
Yanıt : Kap içinde başlangıçta 5 mol gaz olup bu gazın oluşturduğu toplam basınçta 5 atm. dir. Ortama toplam 3 mol daha gaz eklenerek gaz hacmi 8 mole çıkartılmıştır. Bu nedenle sistemin yeni basıncı;
| P_s = ({n_s \over n_i })P_i |
| P_s = ({8.0 \, mol. \over 5.0 \, mol. }) (5 \, atm.) |
| P_s = 8.0 \, atm. |
Herbir gazın kısmi basıncı ise;
| P_{N_2} = ({n_{N_2} \over n_T })P_s |
| P_{N_2} = ({2 \, mol \over 8 \, mol })(8 \, atm. )= 2.0 \, atm. |
| P_{O_2} = ({n_{O_2} \over n_T })P_s |
| P_{O_2} = ({3 \, mol \over 8 \, mol })(8 \, atm. )= 3.0 \, atm. |
| P_{CO_2} = ({n_{CO_2} \over n_T })P_s |
| P_{CO_2} = ({2 \, mol \over 8 \, mol })(8 \, atm. )= 2.0 \, atm. |
| P_{CH_4} = ({n_{CH_4} \over n_T })P_s |
| P_{CH_4} = ({1 \, mol \over 8 \, mol })(8 \, atm. )= 1.0 \, atm. |
Yanıt : Gaz ideal davranış gösterdiğinden;
| PV = nRT |
Gazın mol sayısı,n; n = m/Mort. olacağından;
| M_{ort.} = ({m \over V })({RT \over P })\quad ya da M_{ort.} = \rho ({RT \over P }) |
yazılabilir. Ayrıca gaz karışımının ortalama mol tartısı Mort. için;
| M_{ort.} = \chi_{H_2} M_{H_2} + \chi_{O_2} M_{O_2} \quad \Rightarrow M_{ort.} = \chi_{H_2} M_{H_2} + (1- \chi_{H_2}) M_{O_2} \quad |
yazılabileceğinden;
| \rho ({RT \over P }) = \chi_{H_2} M_{H_2} + (1- \chi_{H_2}) M_{O_2} \quad |
yazılabilir. Böylece değişkenlerin büyüklükleri yerine konursa
| (1.1251\, g. L^{-1}) ({(0.082\, atm. \, L. mol^{-1} \, K^{-1})(300.16 K) \over (1.0 \, atm.) }) = \chi_{H_2} (2.016 \, g. \, mol^{-1}) + (1- \chi_{H_2}) (32.0 \,g. \, mol^{-1} ) |
| \chi_{H_2} \, = 0.144 \quad ve \chi_{O_2} \, = 0.856 |
olarak hesaplanır.
Yanıt : Gaz örneği Vörn. hacmindeki yeri törn. zamanda terk etmiştir. Referans gazda Vref. hacmindeki yeri tref. zamanda terk etmiştir. Referans gaz moleküllerinin hızı için nref. = Vref./tref. ve Mol tartısı bilinmeyen gaz moleküllerinin hızı için nörn. = Vörn./törn. yazılabilir. Böylece;
| { v_{örn.} \over v_{ref.} } = \sqrt { M_{ref.} \over M_{örn.} } |
| { (V_{örn.} / t_{örn.}) \over V_{ref.}/t_{ref.} } = \sqrt { M_{ref.} \over M_{örn.} } |
Burada Vref. = Vörn. = 50 cm3 olduğundan eşitlik bu veriye göre yeniden düzenlenirse;
| { t_{ref.} \over t_{örn.} } = \sqrt { M_{ref.} \over M_{örn.} } |
yazılabilir. Böylece Mörn. ;
| M_{örn.} = M_{ref.} ({ t_{örn.} \over t_{ref.} })^2 |
sayısal büyüklükler eşitlikte yerine konursa;
| M_{örn.} = (32.00 \, g. mol^{-1}) {({ 25 \, s. \over 27.7 \, s.} })^2 = 26.066 \, g. \, mol^{-1} |
Yanıt : Bir sıcaklık (25 oC) ve bir gaz için (H2) en olasılıklı hız, ortalama hız için ve hız kareleri ortalamalı karekökü hızı için aşağıdaki hesaplama kullanılabilir. Diğer sıcaklık ve gazlar için hız dağılımları aşağıdaki şekilde yapılabilir.
| u_{mp} = \sqrt { 2RT \over M } |
| u_{mp} = \sqrt { 2(8.314\times 10^7 \, erg \, mol^{-1} \,K^{-1})(298.16 \,K) \over 2.016 \, g. \,mol^{-1} }\, = 1568 \, m \, s^{-1} |
| \overline u = \sqrt { 8RT \over \pi M } |
| \overline u = \sqrt { 8(8.314\times 10^7 \, erg \, mol^{-1} \,K^{-1})(298.16 \,K) \over (3.14)(2.016 \, g. \,mol^{-1}) }\, = 1770 \, m \, s^{-1} |
| \sqrt {\overline u^2} = \sqrt { 3RT \over M } |
| \sqrt {\overline u^2} = \sqrt { 3(8.314\times 10^7 \, erg \, mol^{-1} \,K^{-1})(298.16 \,K) \over (2.016 \, g. \,mol^{-1}) }\, = 1921 \, m \, s^{-1} |
Tablo : Bazı Gazların 25 oC ve 500 oC deki hız dağılımları
| 25 oC |
500 oC |
|||||
| GAZ | ump m s-1 |
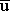 m s-1 |
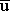(2)1/2 m s-1 |
ump m s-1 |
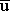m s-1 |
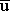(2)1/2 m s-1 |
| H2 | 1568 | 1770 | 1921 | 2525 | 2849 | 3093 |
| He | 1113 | 1256 | 1363 | 1793 | 2023 | 2196 |
| CH4 | 556 | 627 | 681 | 895 | 1010 | 1096 |
| O2 | 394 | 444 | 482 | 634 | 715 | 776 |
Yanıt : Ortalama serbest yol, çarpışma frekansı ve çarpışma hızı için eşitlikleri yeniden yazarak nelere ihtiyacımız olduğunu görelim.
L ={ 1 \over \sqrt 2 \pi d^2 N^*} Bu eşitlikte bilmediğimiz şey birim alandaki tanecik sayısı, N*, dir.
Z1 = 21/2pd2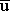N* Burada ihtiyacımız olan şey N* yanısıra, taneciklerin ortalama hızları olan 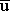değeridir.
Z11 = N*Z1/2 olduğundan öncelikle 1 cm3 teki tanecik sayısını ve 25 oC deki taneciklerin ortalama hızlarını bulalım.
| N^* = {PV \over RT}N_o |
| N^* = {(1 \, atm.)(1\times 10^{-3} \, L.) \over (0.082 \,atm. \,L. \,mol^{-1} \,K^{-1})(298.16 K)}(6.02\times 10^{23} molekül \,mol^{-1}) \,= \, 2.46\times 10^{19} \, molekül |
\overline u_{H_2} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(2.016 \, g. mol^{-1})} = 176952 \, cm \, s^{-1}
\overline u_{He} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(4.00 \, g. mol^{-1})} = 125623 \, cm \, s^{-1}
\overline u_{N_2} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(28.02 \, g. mol^{-1})} = 47464 \, cm \, s^{-1}
\overline u_{O_2} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(32.00 \, g. mol^{-1})} = 44415 \, cm \, s^{-1}
\overline u_{Ar} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(39.948 \, g. mol^{-1})} = 39751 \, cm \, s^{-1}
\overline u_{CO_2} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(44.00 \, g. mol^{-1})} = 37876 \, cm \, s^{-1}
\overline u_{HI} = \sqrt {8(8.314\times 10^7 \, erg \, mol^{-1} \, K^{-1})(298.16 \,K) \over (3.14)(127.90 \, g. mol^{-1})} = 22216 \, cm \, s^{-1}
olarak bulunabilir.L_{(H_2)} = { 1 \over \sqrt 2 \pi d^2 N^*}
L_{(H_2)} = { 1 \over \sqrt 2 (3.14)(2.73\times 10^{-8} \, cm)^2 (2.46\times 10^{19} \, molekül \, cm^{-3})} = 1.23\times 10^{-5} \, cm
Z_{1 (H_2)} = \sqrt 2 \pi d^2_{H_2} \overline u_{H_2} N^*
Z_{1 (H_2)} = \sqrt 2 (3.14) (2.73\times 10^{-8} \, cm)^2 (176952 \, cm \, s^{-1})(2.46\times 10^{19} \,molekül \, cm^{-3})\, = \, 1.44\times 10^{10} \, çarpışma \,s^{-1}
Z_{11 (H_2)} = Z_{1 (H_2)} {N^{*}\over 2}
Z_{11 (H_2)} = (1.44\times 10^{10} \, carpışma \, s^{-1}) {(2.46\times 10^{19} \,molekül \, cm^{-3})\over 2} = 1.78\times 10^{29} \, çarpışma \, cm^{-3}
Benzer hesaplamalar diğer moleküller için yapılacak olursa aşağıdaki tablo görüldüğü gibi doldurulabilir.
Tablo : Bazı Gazların 25 oC ve 1 atm. kinetik moleküler gaz teorisine göre özellikleri
| GAZ | Çarpışma çapı A |
Ortalama Serbest Yol cm(x106) |
Çarpışma Frekansı s-1(x10-9) |
Çarpışma Hızı cm-3s-1(x10-28) |
| H2 | 2.73 | 12.3 | 14.4 | 17.8 |
| He | 2.18 | 19.2 | 6.53 | 8.05 |
| N2 | 3.74 | 6.53 | 7.27 | 8.95 |
| O2 | 3.57 | 7.17 | 6.19 | 7.63 |
| Ar | 3.62 | 6.97 | 5.70 | 7.02 |
| CO2 | 4.56 | 4.40 | 8.62 | 1.06 |
| HI | 5.56 | 2.96 | 7.52 | 9.26 |
Yanıt : Havanın yaklaşık mol tartısı \overline M \,;
\overline M = \chi_{O_2}M_{O_2}+\chi_{N_2}M_{N_2}
eşitliğinden;
\overline M = (0.2)(32.00 \,g \,mol^{-1})+(0.8)(28.04 \,g \,mol^{-1}) = 28.8 \,g \,mol^{-1}
olarak elde edilir.
ln {P \over P_o} = - {Mgz \over RT}
eşitliğinden
ln {P \over 1 atm.} = - {(0.0288 \,kg \,mol^{-1})(9.81 \,m \,s^{-2})(40000 \, m) \over (8.314 \,kg \, m^2 \,s^{-2} \, mol^{-1} \, K^{-1})( 303.16 \,K)}
P = 0.011 atm. olarak hesaplanır.
Yanıt :5555555555555555555555
5555555555555555555555
Yanıt :5555555555555555555555
5555555555555555555555
Yanıt :5555555555555555555555
5555555555555555555555