Gazların Yoğunlaşması, Kritik Nokta ve Karşılıklı Haller İlkesi

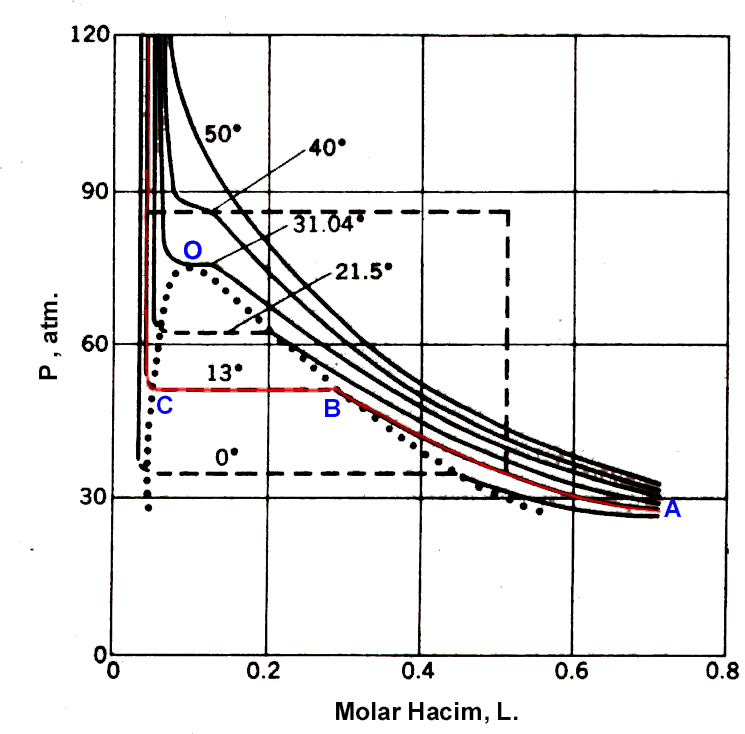
Şekil 1 : Farklı sıcaklıklarda CO2 gazının P-V değişimini gösteren izotermler. Şekil 1 de CO2 in yoğunlaşmasını belirlemek için elde edilmiş bir grup izotermi göstermektedir. Şekildeki veriler gazların davranışları üzerine 1869 da Andrews' in çalışmaları sonucu elde edilmiştir. Yüksek sıcaklıklardaki izotermler, ideal gazlar için beklenen hiperbolik eğrilerden biraz saparlarken, düşük sıcaklık izotermlerinde ise; ideal gaz yasasında önemli ölçüde sapma gösterirler. Düşük basınç değerlerinde ideal gaz davranışı görülür. Belli bir sıcaklıkta basınç arttıkça hacim Boyle Yasası'na uygun şekilde azalır. Şekil 2 : Basınca dayanaklı bir kap içerisinde sıcaklığın yükselmesi ile CO2 in kritik sıcaklık civarındaki davranışı. Şekildeki noktalı çizgilerle gösterilmiş noktaya ulaşıldıktan sonra daha düşük sıcaklıklarda çalışılacak olursa, gazın basıncının arttırılmasıyla gaz sıkışmak yerine yoğunlaşır. Şekilde 21.5, 13 ve 0 oC de yoğunlaşmanın meydana geleceği basınçlar görülmektedir. Şekilden de görüldüğü gibi karbondioksit için kritik değer 31.04 oC dir. Bu sıcaklığın daha altında örneğin şekildeki gibi 13 oC de A noktasındayken basınç arttırılacak olursa B noktasına gelinceye kadar gazın basıncı artar. Bu noktadan sonra gaz sıkıştırılacak olursa basınç değişmeksizin gaz sıvılaşmaya başlar ve C noktasına ulaşılır. Noktalı eğri üzerinde sıvı-buhar birlikte dengededirler diğer bölgelerde yalnızca tek tip akışkan bulunur. Gaz sistemlerin ideal olmayan davranışlarına ilişkin çalışmalardaki ilginç bir yer grafikteki noktalı çizgidir. Bu kritik izoterm olarak adlandırılır. Kritik izotermin sıcaklığı kritik sıcaklıktır. Bu sıcaklık sıvı-buhar dengesinin bulunduğu en yüksek sıcaklıktır. O ile gösterilmiş olan nokta ise kritik noktadır. Bu noktadaki basınç, kritik basınç ve sıcaklık, kritik sıcaklık olarak isimlendirilir. Bazı maddeler ilişkin kritik değerler aşağıdaki Tablo 1 de gösterilmiştir. 1 atm. civarında kuru buz şeklindeki CO2 süblimleşir. Şekil 2 de yüksek basıncı bir kap içinde iken sıvı halde bulunan CO2 kritik sıcaklık civarında gaz ve sıvı arasındaki sınır çizgisi kaybolarak gaz dönüşümü görülmektedir. Tablo 1 : Kritik Noktada P, V ve T değerleri (Gazlar mol tartılarına göre dizilmişlerdir.) Gaz Pc atm. Vc L. Tc K H2 12.8 0.07 33.3 He 2.26 0.062 5.3 CH4 45.6 0.099 190.2 NH3 112.2 0.072 405.6 H2O 217.7 0.056 647.2 CO 35 0.09 134.4 Ne 26.9 0.044 44.8 N2 33.5 0.09 126 NO 65 0.058 179 O2 49.7 0.074 154.4 CH3OH 78.5 0.118 513.1 HCl 81.6 0.087 324.6 Ar 48 0.076 150.7 CO2 72.8 0.094 304.2 SO2 77.7 0.123 430.4 n-C5H12 33 0.31 470.3 Cl2 76.1 0.124 417 C6H6 47.9 0.256 561.6 Kr 54.3 0.107 209.4 Xe 57.9 0.12 289.8 Gerçek gazların ideallikten sapmaları gazın şartları ve kritik nokta arasındaki farka bağımlıdır. Bulunulan P,V, T değerlerini kritik değerlere bağlı olarak ifade edebiliriz. Bu değerler indirgenmiş değişkenler Pr, Vr ve Tr simgeleri ile \rm P_r = { P \over P_c } \; V_r = { V \over V_c } \; ve \; T_r = { T \over T_c } eşitlikleri ile verilir. Eğer kritik değerler bilinirse gazın davranışı kolayca karakterize edilebilir. İndirgenmiş basıncın bir fonksiyonu olarak Z sıkıştırılabilirlik föktörü incelenebilir. Çeşitli indirgenmiş sıcaklıklarda farklı gazlar için yapılmış çalışmalar sonucu Şekil 2 dekine benzer grafikler elde edilir. Bu sonuçlar gazların ideallikten sapmalarının yalnızca indirgenmiş basınç ve sıcaklığa bağlı olduğunu gösterir. Bu ifade karşılıklı haller ilkesini olarak adlandırılır. İfadenin adı, aynı indirgenmiş değişkenlere sahip gazların aynı miktarda ideallikten sapmalarından hareketle verilmiştir. Şekil 2 : Çeşitli gazlar için indirgenmiş basınç değerlerine karşı, farklı indirgenmiş sıcaklıklardaki sıkıştırılabilirlik faktörlerinin uyumu. Gerçek Gazlarla İlgili Bertholet Denklemi Yüksek basınçlarda Bertholet hal denklemiyle gerçek gazların deneysel sonuçları arasında paralellik sağlamak mümkün değildir. Denklem düşük basınçlarda daha uygun değerler vermektedir. Düşük basınçlarda 1 mol gaz için sıkıştırılabilirlik faktörü Z; \rm Z = 1 + {9 \over 128}{ P_r \over T_r} \Big( 1 - { 6 \over T_r^2} \Big) eşitliği ile verilir. PV=ZnRT ifadesinden hareketle ifade \rm PV=nRT \Big[ {9 \over 128}{ P_r \over T_r} \Big( 1 - { 6 \over T_r^2} \Big) \Big] şeklinde düzenlenebilir.