Barometrik Dağılım Yasası
|
Yerçekimi etkisi nedeniyle atmosferde yukarılara doğru çıkıldıkta yoğunluk azalır. Atmosferin üst kısımlarına çıkıldıkça Yerçekimi ivmesinin azalması ve sıcaklığında etkisi ile atmosferin üst kısımlarındaki basınç hızla düşer. Atmosfer basıncını yüksekliğe bağlayan eşitlik barometrik dağılım yasası olarak bilinir.
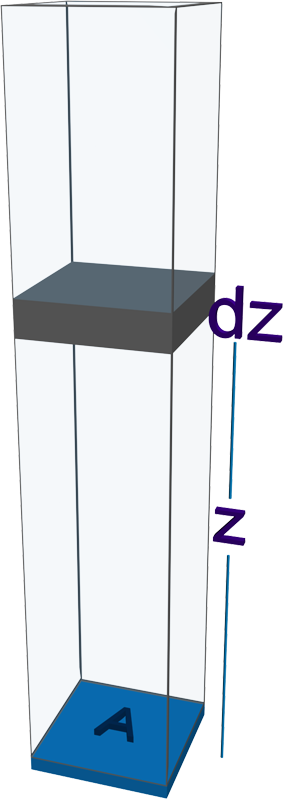
Yandaki şekilde görüldüğü gibi A yüzeyi üzerindeki bulunan bir hava sütunu düşünelim. Bu sütun üzerinde herhangi bir z yüksekliğinde bulunan dz kalınlığındaki bir hava tabakası, g yerçekimine sahip bir yerdeki bu tabakanın yoğunluğu r ise; Bu dz kalınlığındaki havanın ağırlığı rgdz olacaktır. Bu gaz tabakasından alttan üstte doğru gidildikçe gaz basıncının değişimi dP/dz=-rg olacağından, ideal davranış gösterdiği varsayılan gazın yoğunluğu r=PM/RT olacağından; \rm dP = - \rho g dz = - ({PM \over RT})g dz
\rm \int_{P_o}^P {dP\over P} = -\int_{z_o}^z ({Mg \over RT}) dz
zo tabanın değeri sıfır olduğundan; \rm ln {P \over P_o} = - {Mgz \over RT}
elde edilir. Mol tartısı \rm M; \,M = mN, genel gaz sabiti \rm R;\, R = kN dönüşümü yapılırsa; \rm ln {P \over P_o} = - {mgz \over kT}
eşitliği yazılabilir. bir taneciğin potansiyel enerjisi \rm E_p; \, E_p = mgz olacağından son eşitlik; \rm ln {P \over P_o} = - {E_p \over kT}
veya \rm P =P_oe^{ - {E_p \over kT}}
şeklinde yazılabilir. Gaz basıncı yoğunluk veya tanecik sayısı ile doğru orantılı olduğundan \rm ln { \rho \over \rho_o} = - {E_p \over kT}
ya da No; z=0 yüksekliğindeki molekül sayısı ve N'; z=z yüksekliğindeki tanecik sayısı olmak üzere \rm ln {N' \over N_o} = - {E_p \over kT}
veya \rm N' =N_oe^{ - {E_p \over kT}}
eşitliği yazılabilir. Elde edilen bu son eşitlik yalnızca yüksekliğe bağlı olarak gaz moleküllerinin sayısını değil, bir ortamda dağılmış kolloidal taneciklerin sayısını bulmak içinde kullanılabilir. Örneğin; ro yoğunluğundaki bir fazda dağılmış r yoğunluğundaki r yarıçaplı küresel tanecikler için taneciklerin ağırlığı, N Avogadro sayısı olmak üzere \rm Mg = N {4 \over 3}\pi r^3( \rho - \rho_o ) g
Bu sistemin z1 ve z2 yüksekliklerindeki tanecik sayısı N1 ve N2 olmak üzere \rm ln {N_2 \over N_1} = - {N {4 \over 3}\pi r^3( \rho - \rho_o) g (z_2 - z_1 ) \over RT }
eşitliği yazılır.
Barometrik Dağılım Yasası Çözümlü Örnek.
|