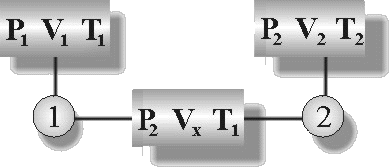
İdeal gazlara ilişkin P=f(V), ve V=f(T) ilişkisinin nasıl olduğunu inceledik. fakat çoğu kez P, V, T aynı anda değişime uğrayabilir. Bu durumda yeni duruma karşı gelen büyüklüklerin ne olduğunu söyleyebilmek için yeni bir eşitliğe ihtiyaç duyabiliriz. Bu iki yasayı birlikte inceleyen ve ilgili değişkenleri bir ifade de bulunduran yasaya da Birleşik Gaz Yasası adı verilir. Birleşik gaz yasasına ilişkin denklemi türetebilmek için aşağıdaki şekli düşünelim.

Burada P1, V1 ve T1 durumundaki sistemin, 1 ve 2 yolundan ilerleyerek P2, V2 ve T2 durumuna ulaştığını varsayalım.
1 nolu basamağı düşünürsek değişen büyüklük basınç ve buna bağlı olarak hacimdir.
Vx/V1 = P1/P2
2 nolu basamağı düşünürsek değişen büyüklük sıcaklık ve buna bağlı olarak yine hacimdir.
V2/Vx = T2/T1
heriki eşitlikteki Vx büyüklüğü birbirine eşitlenirse
(P1V1/P2) = Vx = (T1V2/T2) veya (P1V1/T1) = (P2V2/T2) = k
yazılabilir. (1)
gazın mol sayısı ile ile hacmi doğru orantılı olduğundan k sabitinin değeri belirlenebilir. Aslında buraki k değeri gazın mol sayısını ve genel gaz sabitini içerir. İdeal bir gaz; 1 mol gaz 0 oC de 1 atm. basınç altında 22.413 L hacim kaplar. Böylece;
R = PV/nT
R = [(1.0 atm.)(22.413 L.)]/[(1 mol)(273.15 K)] = 0.08205 atm. L. mol-1 K-1
yazılabilir.
Bir gazın mol tartısını genel gaz denkleminden hareketle hesaplayabiliriz. Gaz örneğinin mol saysı, n, için; n=m/M ve gazın yoğunluğu, d, için; d=m/V yazılırsa, mol tartısı için
M = (d/P)RT
eşitliği elde edilebilir. Gerçek gazlar için yüksek basınçlarda gazın ideallikten saptığını söylemiştik. Bu nedenle; bir gazın mol tartısı doğru olarak hesaplanmak istenirse P --> 0 değerine giderken ortaya çıkan d/P değerinin büyüklüğünden yararlanarak mol tartısının hesaplanması daha az hatalı sonuçların elde edilmesi için önemlidir (1).
Gaz sabiti, R, yalnızca PVT hesaplamalarını kapsamaz. Moleküler sistemlerin enerjileri üzerinde yapılan hesaplamalarda da kullanılır. İş boyutunda R ye bakılacak olursa bu yaklaşım daha az şaşırtıcıdır.

Uzunluk ile kuvvetin çarpımı ise enerjiye karşı gelir. Bu nedenle R nin boyutu, mol kelvin başına enerji büyüklüğünü gösterir. Şimdi R nin sayısal değerini enerjiye bağlı olarak nasıl hesaplayacağımızı gösterelim. Bu amaçla CGS veya MKS birim sistemlerinden birini kullanabiliriz.
1 atmosfer basınç; 1 cm2 kesitinde 76 cm yüksekliğindeki civa kolonunun tabanda oluşturacağı basınç büyüklüğüdür. 0 oC de civanın yoğunluğu 13.595 g cm-3 ve yerçekim ivmesi 980.66 cm s-2 olarak alınacak olursa, gaz sabiti

olarak hesaplanabilir. 1 Joule = 107 erg ve 1 calori= 4.18 Joule olduğundan R nin değeri 8.314 J mol-1 K-1 veya 1.987 cal mol-1 K-1 olarak elde edilebilir.